The fact that the mechanical energy of the driven and damped harmonic oscillator cannot be defined (is infinite) if the damping factor γ is zero, gives us an indication that the damping factor may depend on the angular frequency ω of the driving force.
An expression with respect to a variable damping factor γ(ω) can be taken directly from the formula for the amplitude y0(ω), as follows
where we have supposed that the damping factor γ0 within the expression for the amplitude y0(ω) corresponds to ω=ω0,
In that sense, at resonance, ω=ω0, the damping factor γ(ω0) will not be zero, but equal to the value γ0.
This is graph of the damping factor γ(ω), with respect to the angular frequency ω of the driving force:
The choice of γ0=ω0 is the simplest one (for example we may have set γ0=2ω0). The black dotted lines (of the form y=x and y=1/x) were plotted for comparison.
The important aspect of the previous graph is that the damping factor γ(ω) takes its minimum value at γ0, where ω=ω0, instead of becoming zero. If ω<ω0, then γ(ω) behaves like 1/ω, while if ω>ω0, then γ(ω) behaves like ω (dotted lines in the graph).
The relationship between the damping factor γ(ω) and the amplitude y0(ω) is the following one,
and
where
Here we will derive an expression for the energy of the system with respect to the damping factor γ(ω), if the driving angular frequency ω of the moving object is greater than the natural angular frequency ω0 of the oscillator, ω>>ω0.
In such a case, from the equation which gives the mechanical energy,
we may write,
where
so that we may set
We may notice here that the energy amplitude Em(ω) is twice as much as the average energy amplitude <Em(ω)>,
Now if the angular frequency ω of the driving force is sufficiently larger than the natural frequency ω0 of the oscillator, then we have that
and
The same expression can be directly taken from the expression for the mechanical energy Em(t), if ω>>ω0,
Thus, if the angular frequency ω of the driving force is sufficiently larger than the natural frequency ω0 of the oscillator, then the mechanical energy of the system is purely kinetic energy.
In other words, if we associate the driving force with an object moving with the oscillator, this object will have transformed the available initial elastic energy into its own kinetic energy.
An expression with respect to a variable damping factor γ(ω) can be taken directly from the formula for the amplitude y0(ω), as follows
This is graph of the damping factor γ(ω), with respect to the angular frequency ω of the driving force:
The choice of γ0=ω0 is the simplest one (for example we may have set γ0=2ω0). The black dotted lines (of the form y=x and y=1/x) were plotted for comparison.
The important aspect of the previous graph is that the damping factor γ(ω) takes its minimum value at γ0, where ω=ω0, instead of becoming zero. If ω<ω0, then γ(ω) behaves like 1/ω, while if ω>ω0, then γ(ω) behaves like ω (dotted lines in the graph).
The relationship between the damping factor γ(ω) and the amplitude y0(ω) is the following one,
In such a case, from the equation which gives the mechanical energy,
In other words, if we associate the driving force with an object moving with the oscillator, this object will have transformed the available initial elastic energy into its own kinetic energy.





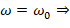































No comments:
Post a Comment