Earlier we saw the approximation for the average amplitude of the mechanical energy, if the damping factor were equal to zero. However if the damping factor depends on the angular frequency of the driving force, γ=γ(ω), then it cannot be zero.
A more interesting case arises if we suppose that the damping factor γ(ω) at resonance, ω=ω0, is equal to 2ω0, thus introducing to the system the condition of critical damping,
where ω΄ is the angular frequency referring to the damping.
On the other hand, we have the condition which maximizes the amplitude y0(ω) of the driven oscillator,
Although the angular frequency ω of the driving force is generally considered that it does not depend on the angular frequency ω΄ of the damping, if we substitute γ0=2ω0 in the latter expression, we take
By taking the absolute value of the condition for the maximum amplitude y0(ω)max, we may suggest that the angular frequency ω of the driving force can be equal to the angular frequency ω0 of the free oscillator from two opposite directions, either if γ=0 (before damping or a driving force is applied), or if γ=2ω0 (when damping and a driving force are applied).
Thus for the driven and damped harmonic oscillator, when we have critical damping, ω΄=0, we also have resonance, ω=ω0.
Substituting now the condition of critical damping, γ0=2ω0, into the formula for the amplitude y0(ω) we take,
The expression in the square root is in fact a perfect square,
Therefore, for the amplitude y0(ω) it will be
so that, for the amplitude of the mechanical energy Em(ω), we have
If additionally ω=ω0, then we have
so that amplitude of the mechanical energy Em(ω) will be half the total mechanical energy E0.
Notes:
If in the expression which gives the amplitude
we set
where κ is the wavenumber, then we take
If in the last expression we add a factor of ½, and assume that that v<<c,
we take back the relativistic expression for the displacement.
Τhe relativistic formula for the displacement can also be taken from the expression for the maximum amplitude of the driven and damped harmonic oscillator,
if we use the following identities,
where we have used the cyclic approximation relating the linear displacement y to the wavelength λ of the oscillator, so that,
Such approximations justify earlier assumptions we made, as in the ship- in- the- sea example, where the Lorentz factor γL appeared with a positive sign,
while the result we previously took
may be considered more complete, as it will be further explored in what follows.
A more interesting case arises if we suppose that the damping factor γ(ω) at resonance, ω=ω0, is equal to 2ω0, thus introducing to the system the condition of critical damping,
On the other hand, we have the condition which maximizes the amplitude y0(ω) of the driven oscillator,
Thus for the driven and damped harmonic oscillator, when we have critical damping, ω΄=0, we also have resonance, ω=ω0.
Substituting now the condition of critical damping, γ0=2ω0, into the formula for the amplitude y0(ω) we take,
Notes:
If in the expression which gives the amplitude
where
Τhe relativistic formula for the displacement can also be taken from the expression for the maximum amplitude of the driven and damped harmonic oscillator,







































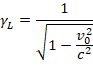





No comments:
Post a Comment