Apart from the numerical coincidences which we saw in the previous section, if in the energy equation of the brachistochrone we replace the mass MB of the brachistochrone with the mass MU of the observable universe, and the radius RB of the brachistochrone with the radius RU of the observable universe, then we take
where the ratio ρ, giving the linear density of the observable universe, was identified in the previous section.
Thus we take as result that the wavelength λ of the reference photon is reduced into Planck length lP.
This result is not obvious, but it is a consequence of the notion of the brachistochrone, and of the energy equation which brings together a pair of phenomenally unrelated quantities, the ratio of the mass MU of the observable universe to Planck mass mP, or, equivalently, the ratio of the radius RU of the observable universe to Planck length lP,
The number NP is a fixed quantity, which we have already calculated in the previous section.
But if we ignore the distinction between the different masses or lengths which appear in the latter formula, then the energy equation reduces to the following undifferentiated form,
and loses its meaning.
Therefore the hypothesis of the brachistochrone is significant in order to take more general results.
In fact such results may offer us a better estimation for the mass MU of the observable universe. The current estimate for this mass is
But here we have that
If we accept this result as more accurate, then the brachistochrone hypothesis can be used in order to give physical meaning to the numerical coincidence of the previous ratio.
Another consequence of such a coincidence is the following one. We have already talked about Schwarzschild radius, which is given by the formula
where RS is the radius of a black hole, and MS is its mass.
This formula can be derived from the mechanical energy of a system, if this energy is gravitational and kinetic energy. Supposing, for example, that an object of mass m leaves the surface of the Earth with a speed v, and is set in orbit around the Earth, then if R is the radius of the orbit, and ME is the mass of the Earth, the conservation of the mechanical energy gives
The speed v is the escape speed of the object from Earth’s gravity. If this speed was equal to the speed of light c, then the Earth would turn into a black hole, and its radius would be given by Schwarzschild’s formula, replacing v by c in the previous equation,
This would be about 10 millimeters.
Now we will see what happens if we replace in Schwarzschild’s formula the mass of the gravitating body with the mass MU of the observable universe.
It would also be helpful to change the units of Newton’s gravitational constant G into light units, as follows
Replacing these values into Schwarzschild’s formula (omitting the factor of 2), we take
Remarkably enough, the value of Schwarzschild radius RS in this case is identical to the radius RU of the observable universe. But since the Schwarzschild radius RS of the universe is (exactly or about) equal to the radius RU of the observable universe, then we must conclude that the universe is a black hole!
An explanation of this coincidence could be that the linear density ρ of the observable universe, which we may also call ρU, is constant,
An observation here is that the (inverse) linear density of the universe ρU numerically coincides with the gravitational constant G (in units of light),
Calculating the product of these two quantities, we have
Therefore, returning to Schwarzschild radius, we take that
Now another interesting aspect arises if we take the following two ratios, which we also saw in the previous section,
If the wavelength λg of the graviton numerically coincides with the speed of light c, then we can write that
Presumably, the quantity ℊ will be constant throughout the universe, since all the related quantities are constants, and will be equal to 1ly/y2.
But the coincidences do not end here. Another observation we can make is that that acceleration of gravity, on the Earth’s surface, which we may call gE, is approximately equal to 1ly/y2, if we change the units into light units as follows,
Another way to express this coincidence is with respect to the linear density ρ or area density σ of the Earth and of the universe. Given the values for the mass ME and radius RE of the Earth, and for the mass MU and radius RU of the observable universe, respectively,
for the linear density ρE and area density σE of the Earth we have,
while for the linear density ρU and area densit σU of the observable universe we have
We can also calculate the corresponding accelerations for those densities,
so that if we identify the acceleration on the Earth’s surface gE with the acceleration ℊ, it will be
Incidentally, the ratio
which has units of angular frequency, gives us Hubble constant,
Hubble constant is estimated to be
where
so that,
Therefore the value of
can be seen as a more accurate estimation of Hubble constant.
Conclusively, from the equation for the acceleration ℊ,
we have the equivalent expressions,
We should mention here that in the calculation of the area density σ we have assumed that the Earth was flat, or perhaps that the Earth’s mass was spread across the surface of a sphere of radius equal to the Earth’s radius (while we have ignored the radian factor π for simplicity). Such assumptions can be based on the holographic principle, which we will explore later on.
The same assumptions can also be based on the brachistochrone hypothesis. As the universe, so the Earth can be seen as a brachistochrone whose mass is either spread across the curve of the brachistochrone, or concentrated on the focus of the brachistochrone. This is as far as the linear density is concerned.
With respect to the area density, we have to suppose that the mass of the brachistochrone is spread within the area of the brachistochrone, thus the region enclosed by the rim L and the curve S of the brachistochrone. The area A of the brachistochrone is in fact A=3πR2, thus analogous to the radius of the brachistochrone squared.
Therefore, ultimately, approximating either the Earth or the universe with a brachistochrone, we take meaningful results which, besides their implication with respect to the appearance of life on Earth (considering for example that the acceleration of 1ly/y2 is ideal for the appearance of life as we know it), apply everywhere.
Incidentally, the acceleration ℊ, which is constant throughout the universe, and (as has been treated here) equal to 1ly/y2, could be identified with a field, yet unknown.
Thus we take as result that the wavelength λ of the reference photon is reduced into Planck length lP.
This result is not obvious, but it is a consequence of the notion of the brachistochrone, and of the energy equation which brings together a pair of phenomenally unrelated quantities, the ratio of the mass MU of the observable universe to Planck mass mP, or, equivalently, the ratio of the radius RU of the observable universe to Planck length lP,
But if we ignore the distinction between the different masses or lengths which appear in the latter formula, then the energy equation reduces to the following undifferentiated form,
Therefore the hypothesis of the brachistochrone is significant in order to take more general results.
In fact such results may offer us a better estimation for the mass MU of the observable universe. The current estimate for this mass is
[https://en.wikipedia.org/wiki/Observable_universe]
But here we have that
Another consequence of such a coincidence is the following one. We have already talked about Schwarzschild radius, which is given by the formula
This formula can be derived from the mechanical energy of a system, if this energy is gravitational and kinetic energy. Supposing, for example, that an object of mass m leaves the surface of the Earth with a speed v, and is set in orbit around the Earth, then if R is the radius of the orbit, and ME is the mass of the Earth, the conservation of the mechanical energy gives
Now we will see what happens if we replace in Schwarzschild’s formula the mass of the gravitating body with the mass MU of the observable universe.
It would also be helpful to change the units of Newton’s gravitational constant G into light units, as follows
An explanation of this coincidence could be that the linear density ρ of the observable universe, which we may also call ρU, is constant,
But the coincidences do not end here. Another observation we can make is that that acceleration of gravity, on the Earth’s surface, which we may call gE, is approximately equal to 1ly/y2, if we change the units into light units as follows,
[https://map.gsfc.nasa.gov/universe/uni_expansion.html]
where
Conclusively, from the equation for the acceleration ℊ,
The same assumptions can also be based on the brachistochrone hypothesis. As the universe, so the Earth can be seen as a brachistochrone whose mass is either spread across the curve of the brachistochrone, or concentrated on the focus of the brachistochrone. This is as far as the linear density is concerned.
With respect to the area density, we have to suppose that the mass of the brachistochrone is spread within the area of the brachistochrone, thus the region enclosed by the rim L and the curve S of the brachistochrone. The area A of the brachistochrone is in fact A=3πR2, thus analogous to the radius of the brachistochrone squared.
Therefore, ultimately, approximating either the Earth or the universe with a brachistochrone, we take meaningful results which, besides their implication with respect to the appearance of life on Earth (considering for example that the acceleration of 1ly/y2 is ideal for the appearance of life as we know it), apply everywhere.
Incidentally, the acceleration ℊ, which is constant throughout the universe, and (as has been treated here) equal to 1ly/y2, could be identified with a field, yet unknown.





























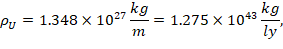














































No comments:
Post a Comment