As we have already said, the graviton may be considered as a special case of a brachiston. The hypothesis of the brachiston can be based on the aspect that masses smaller than the graviton mass are possible.
As far as the graviton is concerned, according to Wikipedia, its mass is estimated as follows: The analysis of gravitational waves yielded a new upper bound on the mass of gravitons, if gravitons are massive at all.
The graviton’s Compton wavelength
is at least 1.6×1016m, or about 1.6 light-years, corresponding to a graviton mass of no more than 7.7×10-23eV/c2.
Recent observations of gravitational waves have put an upper bound of 1.2×10-22eV/c2 on the graviton’s mass.
[https://en.wikipedia.org/wiki/Graviton]
[https://en.wikipedia.org/wiki/Compton_wavelength]
Transforming the units of the graviton mass into kg, we have
This is the upper bound (thus the maximum) of the graviton mass, according to the recent observations.
If we put this value for the graviton mass mg into Compton’s formula for the wavelength, we take
where we changed the units of h in light units, as follows
This will be the lower bound for the graviton’s wavelength λg (minimum wavelength), corresponding to the upper bound of the graviton’s mass mg (maximum mass).
An interesting remark here is that the numerical value of Planck constant h (in light units) is almost identical to the value of the graviton mass mg (in kg):
In fact, if the average wavelength λg of a graviton is exactly 1ly, then these two values will numerically coincide:
While there doesn’t seem to be any specific reason why the wavelength λg of the graviton should be exactly equal to 1ly, such an assumption may offer us a more accurate estimation for the mass mg of the graviton (based on the numerical coincidence between Planck constant and the graviton mass).
Now taking the energy of the brachistochrone, and supposing that its mass MB is equal to the mass of the graviton mg, its radius RB will be
so that
where we have used the value for the graviton’s mass mg corresponding to a graviton’s wavelength λg=1ly.
This result gives us the Schwarzschild’s radius of a black hole with mass equal to the graviton mass.
The aspect here is that we have obtained a size much smaller than Planck radius.
However, a size even smaller can be taken. Supposing that the maximum possible value for a particle’s wavelength can be equal to the radius of the observable universe, which we may call RU, then the minimum possible mass, which we may call mb, for a particle will be
where the radius RU of the observable universe is assumed to be
The corresponding mass mb will be the smallest possible mass in the observable universe.
On the other hand, if the maximum possible mass of a particle is the mass of the observable universe, which we may call MU, then its corresponding wavelength, which we may call lb, will be
This will be the smallest possible size (wavelength) in the observable universe.
Incidentally, the value for the mass MU of the observable universe which was used here is somewhat bigger than the current estimated value, and will be derived later on.
The notation lb, instead of λb, was used in accordance to the notation for Planck length lP (instead of λP), because the values mb and lb do not necessarily refer to the same particle, but to a range of values for different particles. Thus, using the notation (λg, mg) for the wavelength and the mass respectively of the graviton, the particle (lb, MU) will be the smallest but heaviest particle, while the particle (RU, mb) will be the biggest but lightest particle in the universe. In this sense, all such ‘particles,’ from the lightest of them, to the universe itself, may be considered brachistons (thus the index ‘b’).
If we now use the value mb as the mass MB of the brachistochrone, then the corresponding value for the radius RB of the brachistochrone will be,
This result gives us the Schwarzschild’s radius of a black hole with mass equal to a brachiston mass mb. This mass, together with the corresponding size lb, will presumably refer to the smallest and lightest possible object in the universe.
Here is a comparison between the two formulas which have been used in this section, referring to Schwarzschild radius RS, and Compton wavelength, which we may also call λC, respectively:
More general relationships can be taken for the same formulas by using the energy equation of the brachistochrone,
If in the first formula
we equate the mass of the brachistochrone ΜΒ to the mass of the moving object m, and we also equate the speed of the moving object v to the speed of light c, we take back Schwarzschild’s formula.
If in the second formula
we additionally equate the wavelength λ of the reference photon to the radius RΒ (or to the length LΒ) of the brachistochrone, we take back Compton’s formula.
But, in the general case, while the radius RΒ of the brachistochrone does not necessarily refer to a black hole, in the second formula the wavelength λ always refers to the size of the reference photon, not to the dimensions of the moving object of mass m.
Thus the notion of the brachistochrone can be used not only to bring together, but also to distinguish between the various aspects of the problem, either such aspects refer to black holes in the macrocosm, or to Compton wavelengths of particles in the microcosm.
Notes:
As we earlier divided the brachistochrone using the numbers N, NP, and N΄, referring either to the number of photons, Planck lengths, or gravitons which the length LΒ or the mass MΒ of the brachistochrone is composed of respectively, the same can be done with respect to the number of brachistons, which we may call N΄΄, which the mass MΒ of the brachistochrone consists of. Thus we may expand the energy equation of the brachistochrone, as follows
The same equation can be written using the variable notation (without the index n), as follows
where
These are the related quantities,
Some attention is needed with respect to the factor of 2π, whether we refer to the radius RU and the length LU of the observable universe, or to Planck radius rP and Planck length lP. Also the quantities mb and lb in general depend on the radius RB and the mass MB of the brachistochrone, respectively.
Thus we have,
Therefore the radius RU of the observable universe consists of NP≈1061 Planck lengths, while the mass MU of the observable universe is composed of N΄≈10111 graviton masses mg, or N΄΄≈10121 brachiston masses mb.
Additionally, we have the following ratios,
Since the related quantities are constants, the ratios Ɲ΄ and Ɲ΄΄ will also be constant.
Here we can mention the following interesting things. Firstly, taking the ratio,
we see that the value for the mass MU of the observable universe can be taken from first principles (supposing, for example, that the radius RU of the observable universe, as well as the values for Planck mass mP and Planck length lP, are given). Incidentally, the quantity ρ has units of linear density.
Secondly, taking the ratio
we see that if this ratio numerically coincides with the radius RU of the observable universe, then the mass mg and the wavelength λg of the graviton will numerically coincide with Planck constant h and the speed of light c, respectively.
Finally, with respect to the speed, if we suppose that the object moving on the brachistochrone is a brachiston of mass mb, while the brachistochrone is the universe itself, then from the energy equation we have that,
Presumably, this will be the maximum possible speed in the observable universe.
As far as the graviton is concerned, according to Wikipedia, its mass is estimated as follows: The analysis of gravitational waves yielded a new upper bound on the mass of gravitons, if gravitons are massive at all.
The graviton’s Compton wavelength
Recent observations of gravitational waves have put an upper bound of 1.2×10-22eV/c2 on the graviton’s mass.
[https://en.wikipedia.org/wiki/Graviton]
[https://en.wikipedia.org/wiki/Compton_wavelength]
Transforming the units of the graviton mass into kg, we have
If we put this value for the graviton mass mg into Compton’s formula for the wavelength, we take
An interesting remark here is that the numerical value of Planck constant h (in light units) is almost identical to the value of the graviton mass mg (in kg):
Now taking the energy of the brachistochrone, and supposing that its mass MB is equal to the mass of the graviton mg, its radius RB will be
This result gives us the Schwarzschild’s radius of a black hole with mass equal to the graviton mass.
The aspect here is that we have obtained a size much smaller than Planck radius.
However, a size even smaller can be taken. Supposing that the maximum possible value for a particle’s wavelength can be equal to the radius of the observable universe, which we may call RU, then the minimum possible mass, which we may call mb, for a particle will be
On the other hand, if the maximum possible mass of a particle is the mass of the observable universe, which we may call MU, then its corresponding wavelength, which we may call lb, will be
Incidentally, the value for the mass MU of the observable universe which was used here is somewhat bigger than the current estimated value, and will be derived later on.
The notation lb, instead of λb, was used in accordance to the notation for Planck length lP (instead of λP), because the values mb and lb do not necessarily refer to the same particle, but to a range of values for different particles. Thus, using the notation (λg, mg) for the wavelength and the mass respectively of the graviton, the particle (lb, MU) will be the smallest but heaviest particle, while the particle (RU, mb) will be the biggest but lightest particle in the universe. In this sense, all such ‘particles,’ from the lightest of them, to the universe itself, may be considered brachistons (thus the index ‘b’).
If we now use the value mb as the mass MB of the brachistochrone, then the corresponding value for the radius RB of the brachistochrone will be,
Here is a comparison between the two formulas which have been used in this section, referring to Schwarzschild radius RS, and Compton wavelength, which we may also call λC, respectively:
If in the second formula
But, in the general case, while the radius RΒ of the brachistochrone does not necessarily refer to a black hole, in the second formula the wavelength λ always refers to the size of the reference photon, not to the dimensions of the moving object of mass m.
Thus the notion of the brachistochrone can be used not only to bring together, but also to distinguish between the various aspects of the problem, either such aspects refer to black holes in the macrocosm, or to Compton wavelengths of particles in the microcosm.
Notes:
As we earlier divided the brachistochrone using the numbers N, NP, and N΄, referring either to the number of photons, Planck lengths, or gravitons which the length LΒ or the mass MΒ of the brachistochrone is composed of respectively, the same can be done with respect to the number of brachistons, which we may call N΄΄, which the mass MΒ of the brachistochrone consists of. Thus we may expand the energy equation of the brachistochrone, as follows
The purpose here is to estimate the maximum value of the numbers NP, N΄, and N΄΄ at the highest possible state n, supposing that this state is given by substituting the radius RB (or the length LB) of the brachistochrone with the radius RU of the observable universe, and the mass MB of the brachistochrone with the mass MU of the observable universe.
These are the related quantities,
Thus we have,
Additionally, we have the following ratios,
Here we can mention the following interesting things. Firstly, taking the ratio,
Secondly, taking the ratio
Finally, with respect to the speed, if we suppose that the object moving on the brachistochrone is a brachiston of mass mb, while the brachistochrone is the universe itself, then from the energy equation we have that,













































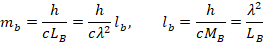






























No comments:
Post a Comment