Here we will show how the relativistic expression for length contraction, or time dilation, can be derived in a physical context, thus with respect to some medium, which, while in the general case we can identify with spacetime, in the special case of this example will be the sea itself.
Motion in the sea is in fact an oscillatory motion, as the ship follows the oscillations of the waves. Usually we ignore the curvature (amplitude) of the sea waves, thus we also ignore the effect of time dilation related to the period of the waves. Instead we estimate the time arrival of the ship as if the ship were travelling on a straight line (in fact this is true only if we travel at a speed equal to the speed of the waves). However if, for example, the sea is rough, so that the amplitude of the waves is large, the effect of time dilation can be significant.
In order to describe the problem, this is a related graph:
According to the previous picture, the ship is initially located at point O, on the crest of the wave. An observer on board the ship measures the period T of the wave at rest (when the ship has no speed of its own). If the speed of the wave is c, then at a time equal to Τ/2 the wave moves a linear distance OD=c(ΔΤ/2) (half a wavelength). As the ship begins to move at a speed v, the period of the wave changes to T΄, according to an observer on board the ship. Presumably, if there was no wave, after a time interval Δt/2, as measured by the clock of the observer, equal to the period ΔT/2 of the wave at rest, the ship would have traveled a horizontal distance OD=v(ΔΤ/2). But because the wave is oscillating, the ship is delayed by the vertical distance DD΄=c(T΄/2) of the oscillation.
Here the distances are measured with respect to the period of the waves,
Thus the time dilation is given as follows,
This result is identical to that in Einstein’s train thought experiment, if we replace the periods T and T΄ by the coordinate times t and t΄, respectively, of two observers.
However there is one basic exception. The times T and T΄ refer to the periods of the wave (the medium), not to the period of photons (the time it takes photons to travel the distances).
Thus the effect of time dilation (or length contraction) can be directly attributed to the motion of the medium (even at conventional speeds). Therefore the relativistic formula, which we have already seen in previous sections, finds here a physical meaning.
This meaning is in accordance with the common experience we have when moving in the sea, that the frequency of the waves which come to us increases (or that the period, thus also their wavelength, decreases).
Incidentally, in the previous description, it was assumed that the speed of the sea waves was c. But if we replace the sea with spacetime, then, supposedly, the speed c will be the speed of light.
That spacetime may produce waves is not absurd. If there is energy stored in spacetime, then this energy will be expressed with some form of oscillations, therefore there will be a wave associated with spacetime.
Sea waves are in fact gravitational waves (so that water helps us perceive these waves with our own eyes). Thus spacetime can be seen as a gravitational wave, composed by gravitons instead of molecules of water.
That the oscillation of such a medium also produces photons- by which in fact we can measure the spatial and temporal properties of the oscillating medium- also poses the question which is the relationship between gravitons and photons. An attempt to answer this question will be made later on, after we introduce the notion of the brachistochrone.
Finally, the intimate relationship between the periods T and T΄ of the medium (spacetime) and the coordinate times t and t΄, of two observers at rest and in motion, respectively, also exposes the deeper connection between physical reality and our own experience of the same reality. Such a connection will be explored at the end of this document.
Notes:
A way to measure a gravitational wave is using an interferometer, which oscillates as the gravitational wave passes by. If the interferometer is placed at point O (previous picture), then, if d is the amplitude of the gravitational wave, the instrument will be displaced at point O΄. The displacement, thus also the amplitude of the gravitational wave, is measured in relation to the distances (spacetime intervals) OA and O΄A. These distances are associated with photons, and with the times t and t΄, respectively, it takes the photons to travel the distances. Thus the amplitude of the gravitational wave will be
If we also assume that the gravitational wave oscillates at the speed of light c, then, if T is the period of the gravitational wave, it will be
In that sense, the time as measured by the observer who uses the interferometer can be defined with respect to the period of the gravitational wave.
Similarly, the two times t and t΄ can be related to two different observers, located at points (reference frames) O and O΄, respectively. If d is the amplitude difference of the gravitational wave between those two points, then the previous equation will give the time difference on the clocks of the two observers.
If we now attribute the gravitational wave to the motion of an object (which produces the gravitational wave by its motion), and relate the two times t and t΄ to the period of photons with which the location of the object is measured, then we go back to the case of the ship in the sea, as earlier described.
Motion in the sea is in fact an oscillatory motion, as the ship follows the oscillations of the waves. Usually we ignore the curvature (amplitude) of the sea waves, thus we also ignore the effect of time dilation related to the period of the waves. Instead we estimate the time arrival of the ship as if the ship were travelling on a straight line (in fact this is true only if we travel at a speed equal to the speed of the waves). However if, for example, the sea is rough, so that the amplitude of the waves is large, the effect of time dilation can be significant.
In order to describe the problem, this is a related graph:
Illustration of the ship- in- the- sea thought experiment
According to the previous picture, the ship is initially located at point O, on the crest of the wave. An observer on board the ship measures the period T of the wave at rest (when the ship has no speed of its own). If the speed of the wave is c, then at a time equal to Τ/2 the wave moves a linear distance OD=c(ΔΤ/2) (half a wavelength). As the ship begins to move at a speed v, the period of the wave changes to T΄, according to an observer on board the ship. Presumably, if there was no wave, after a time interval Δt/2, as measured by the clock of the observer, equal to the period ΔT/2 of the wave at rest, the ship would have traveled a horizontal distance OD=v(ΔΤ/2). But because the wave is oscillating, the ship is delayed by the vertical distance DD΄=c(T΄/2) of the oscillation.
Here the distances are measured with respect to the period of the waves,
However there is one basic exception. The times T and T΄ refer to the periods of the wave (the medium), not to the period of photons (the time it takes photons to travel the distances).
Thus the effect of time dilation (or length contraction) can be directly attributed to the motion of the medium (even at conventional speeds). Therefore the relativistic formula, which we have already seen in previous sections, finds here a physical meaning.
This meaning is in accordance with the common experience we have when moving in the sea, that the frequency of the waves which come to us increases (or that the period, thus also their wavelength, decreases).
Incidentally, in the previous description, it was assumed that the speed of the sea waves was c. But if we replace the sea with spacetime, then, supposedly, the speed c will be the speed of light.
That spacetime may produce waves is not absurd. If there is energy stored in spacetime, then this energy will be expressed with some form of oscillations, therefore there will be a wave associated with spacetime.
Sea waves are in fact gravitational waves (so that water helps us perceive these waves with our own eyes). Thus spacetime can be seen as a gravitational wave, composed by gravitons instead of molecules of water.
That the oscillation of such a medium also produces photons- by which in fact we can measure the spatial and temporal properties of the oscillating medium- also poses the question which is the relationship between gravitons and photons. An attempt to answer this question will be made later on, after we introduce the notion of the brachistochrone.
Finally, the intimate relationship between the periods T and T΄ of the medium (spacetime) and the coordinate times t and t΄, of two observers at rest and in motion, respectively, also exposes the deeper connection between physical reality and our own experience of the same reality. Such a connection will be explored at the end of this document.
Notes:
A way to measure a gravitational wave is using an interferometer, which oscillates as the gravitational wave passes by. If the interferometer is placed at point O (previous picture), then, if d is the amplitude of the gravitational wave, the instrument will be displaced at point O΄. The displacement, thus also the amplitude of the gravitational wave, is measured in relation to the distances (spacetime intervals) OA and O΄A. These distances are associated with photons, and with the times t and t΄, respectively, it takes the photons to travel the distances. Thus the amplitude of the gravitational wave will be
Similarly, the two times t and t΄ can be related to two different observers, located at points (reference frames) O and O΄, respectively. If d is the amplitude difference of the gravitational wave between those two points, then the previous equation will give the time difference on the clocks of the two observers.
If we now attribute the gravitational wave to the motion of an object (which produces the gravitational wave by its motion), and relate the two times t and t΄ to the period of photons with which the location of the object is measured, then we go back to the case of the ship in the sea, as earlier described.










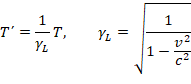






No comments:
Post a Comment