An interesting case arises if the damping angular frequency ω΄ is equal to zero (critical damping). Taking the condition,
and setting ω΄=0, we have,
so that from the equation of motion
we have the following solution,
At time t=0, we have
Accordingly, the energies at time t=0 will be,
Therefore, the total energy will be
where the last term refers to the mass μ0 of the oscillator.
We may notice that if the final speed v0 of the object (‘hanging’ from the oscillator) is equal to the speed of light c (assuming that this is the speed of the oscillator) then it will be
so that the moving object will have consumed a mass equal to the mass per wavelength of the oscillator, as soon as it reaches the speed of light.
At any time t, the energies will be
The last equation can be written simply as
Thus when critical damping is applied, the energy of the system is unified by a common expression for the different forms of energies.
Notes:
This is a comparison between the energy of the damped oscillator, and the energy in relativity.
In the ‘wet sponge’ example, we saw that if the damping factor γ changes with time,
then we take for the mass of the object an expression of the form
Here we can make a similar assumption with respect to the energy of the damped oscillator,
so that setting, for example,
we have for the energy that
In this equation, the energy has the form of a Gaussian function.
If we raise both terms to the power of two (in order to make the ½ factor disappear), we have
The linear (or better the second order) approximation of the previous exponential, at v≈0, v<<c, is
so that
and we take back the relativistic expression for the energy.
This is a related graph:
The red line is the relativistic energy in the form of
while the green line is the exponential energy in the Gaussian form
where E0≈c≈1 in the graph.
The basic aspect here is that while the relativistic energy will be zero if the speed v of the object is equal to the speed of light c, the energy in the Gaussian form will be zero if the speed v of the object is infinite.
This is another way to suggest a correction to the relativistic expression.
We may notice that if the final speed v0 of the object (‘hanging’ from the oscillator) is equal to the speed of light c (assuming that this is the speed of the oscillator) then it will be
At any time t, the energies will be
Notes:
This is a comparison between the energy of the damped oscillator, and the energy in relativity.
In the ‘wet sponge’ example, we saw that if the damping factor γ changes with time,
If we raise both terms to the power of two (in order to make the ½ factor disappear), we have
This is a related graph:
The red line is the relativistic energy in the form of
The basic aspect here is that while the relativistic energy will be zero if the speed v of the object is equal to the speed of light c, the energy in the Gaussian form will be zero if the speed v of the object is infinite.
This is another way to suggest a correction to the relativistic expression.












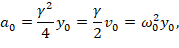

































No comments:
Post a Comment