A way to treat the previous problem, that Lorentz factor goes to infinity if an object moves at the speed of light, is to make the distinction between the coordinate time (the time passing on the clocks of observers), and the period of the photons (the time ‘on the clock’ of the photons).
This is a related sketch:
Here we have the same observer (instead of two), moving on the horizontal axis x=(OO΄). The observer uses photons to estimate the distance he/she travels. Initially the observer is at rest, at point O. The photon is reflected at point O΄, and returns to the observer when he/she is at point A. If it originally takes the photon a time T1 to travel the distance OO΄, this distance will be OO΄=cT1. If the observer travels at a speed v, then, after some time Δt, according to his/her own clock, he/she will have traveled a distance OA=vΔt. During the same time Δt, the photon will have traveled a total distance OO΄+O΄A, where O΄A=cT2, till the observer takes back the photon at point A.
Presumably, the times T1 and T2 refer to the period of the photon, so that the lengths λ1=cT1 and λ2=cT2 will be wavelengths. The distance the observer travels can also be called Δx, so that we have,
The time Δt it takes the observer to reach point A, will be equal to the time T1 it takes the photon to travel from point Ο to point O΄, plus the time T2 it takes the photon to reach point A from point O΄,
Thus for the distances we have,
This formula relates the displacement Δx=vΔt of the observer, to the displacement Δλ=cΔT of the reference (the emitted) photon.
The fundamental aspect here is that, while the time Δt refers to the clock of the observer, the times T1 and T2 refer to the period of the photons.
The time t, as measured by the clock of the moving observer, although still a ‘related’ time, it is not a ‘relative’ time, because it does not refer to an external observer, but it is intimately connected to the period T of the photon itself.
On the other hand, the period of the photon depends on the motion of the observer. In other words, the photon changes its period, because of the motion of the observer,
The dependence of the photon’s period on the speed of the observer, also tells us that the motion (i.e. the speed) of the observer cannot be defined independently of the photon,
Thus the motion of the observer is intimately related to the aspects of the photon. However this relationship involves the photon and the same observer. Therefore the motion is not relative (it does not refer to an external observer), but absolute (it refers to the photon as the medium in which motion occurs).
The most profound interpretation of such an effect is that the photon is not a ‘point (a particle) travelling in empty spacetime,’ but that in fact it is a disturbance of spacetime, which in turn is caused by the motion of the observer. Such an aspect will be significant in our discussion.
This is a related sketch:
Here we have the same observer (instead of two), moving on the horizontal axis x=(OO΄). The observer uses photons to estimate the distance he/she travels. Initially the observer is at rest, at point O. The photon is reflected at point O΄, and returns to the observer when he/she is at point A. If it originally takes the photon a time T1 to travel the distance OO΄, this distance will be OO΄=cT1. If the observer travels at a speed v, then, after some time Δt, according to his/her own clock, he/she will have traveled a distance OA=vΔt. During the same time Δt, the photon will have traveled a total distance OO΄+O΄A, where O΄A=cT2, till the observer takes back the photon at point A.
Presumably, the times T1 and T2 refer to the period of the photon, so that the lengths λ1=cT1 and λ2=cT2 will be wavelengths. The distance the observer travels can also be called Δx, so that we have,
The fundamental aspect here is that, while the time Δt refers to the clock of the observer, the times T1 and T2 refer to the period of the photons.
The time t, as measured by the clock of the moving observer, although still a ‘related’ time, it is not a ‘relative’ time, because it does not refer to an external observer, but it is intimately connected to the period T of the photon itself.
On the other hand, the period of the photon depends on the motion of the observer. In other words, the photon changes its period, because of the motion of the observer,
The most profound interpretation of such an effect is that the photon is not a ‘point (a particle) travelling in empty spacetime,’ but that in fact it is a disturbance of spacetime, which in turn is caused by the motion of the observer. Such an aspect will be significant in our discussion.









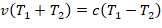








No comments:
Post a Comment