This is an example of how we may relate the journey of an object on the brachistochrone to the properties of a photon:
Suppose that a spaceship (black arrow) leaves point O, and travels accelerating on the brachistochrone OC΄O΄ (orange curve), towards point C΄. In the beginning of the journey, an observer on the spaceship emits a photon, which travels on the straight line ΟC΄ (black dotted line). What is the condition that the observer takes back the emitted photon at the end of the journey, at point C΄?
This is an analysis of the problem:
On one hand, we have the motion of the spaceship. Because the spaceship is accelerating, its path will be that of a brachistochrone, since this is the path of least action (time). Thus it will be the curve OC΄.
On the other hand, the emitted photon will travel on a straight line, since its speed (the speed of light) is constant, thus the photon does not have any acceleration. If we assume that the photon propagates as a spherical (or plane) wave, then the linear path Δr=OC΄ will be the radius of such a wave. Incidentally, the same distance can also be seen as a vector, whose origin is at point O, its end is at point C΄, and whose measure is Δr=cΔt.
The relationship between the curved and linear path OC΄ is that between an arc and a chord, respectively, joining the points OC΄. These two distances, as we have already seen, are given as follows. Calling ΔS the curved path (the arc) OC΄, Δr the linear path (the chord) OC΄, Δx the distance OC, and Δy the distance CC΄, we have
Now the time T is in fact the time of the brachistochrone. This time is given by the formula
Here, to simplify things, we will make the following assumptions. First of all the harmonics n of a photon, as we have already seen, are given as
The difference in the wavelengths is
Now if we also suppose that at the first harmonic of the photon, n=1, the spaceship travels the distance ΔS at the speed of light c, then calling v0 the speed of the spaceship corresponding to the first harmonic, n=1, and vn its speed corresponding to any harmonic n, and since we have identified the speed v0 of the spaceship at the first harmonic, n=1, with the speed of light c, v0=c, we have
Multiplying the previous equation by the harmonic n, we can also identify the time of the brachistochrone Tn, at any harmonic n, with the period of the emitted photon τn, at the same harmonic n,
But how is it is possible that the spaceship (moving faster than light) reaches the end of the journey, at point C΄, before the emitted photon reaches the same point?
If the photon is treated as a ‘point’ which travels all the distance in between, then this is impossible, because causality will be violated. In other words, if the photon is the carrier of the information (thus it also contains the information about the journey of the spaceship) then the spaceship cannot reach point C΄ before the information of its own arrival reaches the same point.
However, if the photon is treated as a disturbance of spacetime, produced by the oscillations of spacetime, then the emitted photon will be located wherever the spaceship is located at a given time. This is because, since the spaceship travels in spacetime, the observer on the spaceship can measure the oscillations of spacetime (in the form of photons) at the same point. The difference is that the period of the photon will change if the spaceship is in motion, because the period of the photon depends on the speed of the spaceship.
Thus, to answer the question in the original problem, the observer on the spaceship will always take back the reference, or ‘emitted,’ photon.
Here is a scheme which shows the difference in the first principles, if we consider spacetime as empty, so that photons are particles which travel in empty space on straight lines, or if we consider spacetime as the medium in which motion occurs, while photons are disturbances of the medium:
On one hand, we have that:
Spacetime is empty.
The observer emits a photon in spacetime.
The photon is a particle which travels on a straight line at the speed of light.
If the observer exceeds the speed of light, he/she will never take back the photon (and causality is violated).
On the other hand, we have that:
Spacetime is an oscillating medium.
The observer can measure the oscillations of spacetime in the form of photons.
The motion of the observer in spacetime disturbs spacetime.
The observer receives the disturbance as a photon with altered period.
As far as the previous condition of simultaneity is concerned,








































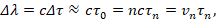




No comments:
Post a Comment