Figure: Two photons are entangled, and travel on the horizontal axis x in opposite directions. The entanglement is achieved by a signal (a brachiston) travelling on the curved line (the brachistochrone) which connects the two photons. The time it takes the two photons to interact is the time of the brachistochrone.
In the previous picture, all the curves Sn (brachistochrones) are also tautochrones (brachistochrone= shortest time, tautochrone= same time). This is not the same brachistochrone, on which different objects end up at the bottom at the same time from different heights, but different brachistochrones, on which the same object reaches the bottom of each brachistochrone, supposedly, at different time.
According to experiments on quantum entanglement, the two entangled particles communicate one with the other ‘instantaneously.’ However the time of the brachistochrone may offer the opportunity to measure such ‘instantaneity’ (supposing that the time can be very small, but not zero).
The photons travel on the linear path Δxn (the interval [-xn…xn] in the previous graph), so that if it takes for a photon a time Δtn to travel this distance at the speed of light c, and each interval Δxn is n times bigger than the initial interval Δx1, then we have that,
where
On the other hand, the brachiston will travel on the curved line Sn, which connects the two ends of the linear distance Δxn, so that, in general, it will be
where v is the speed of the brachiston, and T is the time of the brachistochrone.
The advantage of having introduced the notion of the brachistochrone, is that each brachistochrone Sn is directly related to the length of the brachistochrone Ln, where the length Ln corresponds to the distance Δxn by which the two entangled photons are separated at some time interval Δtn,
For simplicity we will assume that the length of the brachistochrone Sn is analogous to the length of the brachistochrone’s rim Ln, so that
The problem here is that we have to define some initial condition, referring to the separation Δx1 (the interval [-x1…x1] in the previous graph) between the two photons. This can be done if we assume that at the initial separation, L1=Δx1=cΔt1, the brachiston will have to travel as fast as the speed of light, so that the photons are also initially entangled. Thus, it will be
Therefore, due to the initial condition, the time of the brachistochrone T1, will be equal to the time t1 of the photon.
As the photons fly apart from each other, the distance Ln will increase,
As a consequence, the speed vn of the brachiston will be n times greater than the speed of the photons c, as the separation Ln increases by a factor of n.
This can be done without violating causality, as the brachiston (although travelling faster than light) will meet the photon (the carrier of information) at the end of the journey.
Another problem is to define some acceleration g, in relation to the time of the brachistochrone T, which by definition is
where R is the radius of the brachistochrone.
Solving for the initial separation L1, we have
Defining the speed vn,
in such a way that the speed of light c stays constant,
we may also solve the time of the brachistochrone Tn for some final separation Ln,
where
so that
The formulas above relate different parameters of the system to each other, taking into account the given initial condition.
Incidentally, the same formula can be derived if we consider an energy equation of the form,
where the factor of ½ in front of the kinetic energy was dropped for simplicity, and
where
Additionally, we have the properties related to the photons, given by the equation
where λ is the photon’s wavelength, and τ is its period.
If, in addition to the initial condition that the initial speed v1 of the brachiston which entangles the two photons is the speed of light c,
we also assume that the initial separation L1 of the photons is comparable to their wavelength λ1, then it will be
so that, for some final separation Ln, we have that
and
The last equation represents a condition of simultaneity, or synchronicity.
The aspect that the photons’ period τn decreases, while their harmonic n increases, is a consequence of the definitions and assumptions given above.
This can also be seen from the last equation, where the speed of the brachiston vn is inversely proportional to the period of the photon τn, since their product is constant.
A more general relationship between the same two parameters, vn and τn, can be taken if we assume an energy equation of the form,
The last equation shows that the period of the photon τn, is inversely proportional to the speed of the brachiston vn.
If here we set
so that we retrieve the condition of synchronicity we met earlier.
Notes:
The main point is that we cannot define the time of the brachistochrone, thus the time of the entanglement, independently of the photons, that is their wavelength, or period.
This can be seen if we add another energy term of the form Mc2, and using the indices ‘B’ for ‘Brachistochrone,’ and ‘p’ for ‘photon,’ so that
where the mass MB refers to the mass of the brachistochrone (the mass in the region of spacetime where the object of mass m travels).
Replacing
and identifying the acceleration g with the common gravitational acceleration,
we have
Thus the time of the brachistochrone TB will be
where λp and τp is respectively the wavelength and period of the reference (the entangled) photons, and ħ is (the reduced) Planck constant.
If in the last relationship we substitute
where tP is Planck time, we take
This is a simple formula to estimate the time it takes for the entanglement to occur.
This time however cannot be defined independently of the period of the entangled photons. Thus the problem is how one can measure such period, since, presumably, it will be extremely low (even smaller than Planck time), if the time of the entanglement TB is miniscule.
As far as the aforementioned energy relationships are concerned, they will become clearer after the energy of the brachistochrone is introduced.
In the previous picture, all the curves Sn (brachistochrones) are also tautochrones (brachistochrone= shortest time, tautochrone= same time). This is not the same brachistochrone, on which different objects end up at the bottom at the same time from different heights, but different brachistochrones, on which the same object reaches the bottom of each brachistochrone, supposedly, at different time.
According to experiments on quantum entanglement, the two entangled particles communicate one with the other ‘instantaneously.’ However the time of the brachistochrone may offer the opportunity to measure such ‘instantaneity’ (supposing that the time can be very small, but not zero).
The photons travel on the linear path Δxn (the interval [-xn…xn] in the previous graph), so that if it takes for a photon a time Δtn to travel this distance at the speed of light c, and each interval Δxn is n times bigger than the initial interval Δx1, then we have that,
where v is the speed of the brachiston, and T is the time of the brachistochrone.
The advantage of having introduced the notion of the brachistochrone, is that each brachistochrone Sn is directly related to the length of the brachistochrone Ln, where the length Ln corresponds to the distance Δxn by which the two entangled photons are separated at some time interval Δtn,
As the photons fly apart from each other, the distance Ln will increase,
This can be done without violating causality, as the brachiston (although travelling faster than light) will meet the photon (the carrier of information) at the end of the journey.
Another problem is to define some acceleration g, in relation to the time of the brachistochrone T, which by definition is
Solving for the initial separation L1, we have
Incidentally, the same formula can be derived if we consider an energy equation of the form,
If, in addition to the initial condition that the initial speed v1 of the brachiston which entangles the two photons is the speed of light c,
The aspect that the photons’ period τn decreases, while their harmonic n increases, is a consequence of the definitions and assumptions given above.
This can also be seen from the last equation, where the speed of the brachiston vn is inversely proportional to the period of the photon τn, since their product is constant.
A more general relationship between the same two parameters, vn and τn, can be taken if we assume an energy equation of the form,
If here we set
equating thus, for some reason, the mass m of the brachiston, to the mass-equivalent of a region of spacetime of size λ1, we take
Notes:
The main point is that we cannot define the time of the brachistochrone, thus the time of the entanglement, independently of the photons, that is their wavelength, or period.
This can be seen if we add another energy term of the form Mc2, and using the indices ‘B’ for ‘Brachistochrone,’ and ‘p’ for ‘photon,’ so that
Replacing
If in the last relationship we substitute
This time however cannot be defined independently of the period of the entangled photons. Thus the problem is how one can measure such period, since, presumably, it will be extremely low (even smaller than Planck time), if the time of the entanglement TB is miniscule.
As far as the aforementioned energy relationships are concerned, they will become clearer after the energy of the brachistochrone is introduced.








































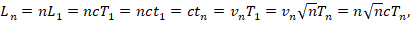























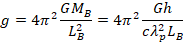





No comments:
Post a Comment