Up till now we have used the terms ‘harmonic’ (referring to the harmonic n of the reference photon), and ‘state’ (referring to the brachistochrone) indiscriminately. For example, in the previous section, it was supposed that the number of photons which fit in the length of the brachistochrone L0, at some harmonic n, is equal to that number n. However this is not necessarily true. More generally, if N0 is the number of photons of wavelength λ0 which fit in the length L0 of the brachistochrone at the first harmonic, n=1, and Nn is the number of photons of wavelength λn which fit in the length L0 of the brachistochrone at some harmonic, n, then it will be
This helps us distinguish between the energy En, at some state n, and the energy per wavelength λn, which we may call εn, at the same state,
Defining now an energy ε0 per photon of wavelength λ0, then for the first harmonic, or state, n=1, it will be
and the total energy at the first state can also be written as,
Similarly, for any state n, the energy εn per photon of wavelength λn will be
so that the total energy at the same state n will be,
Therefore the energy equations can be written in the following general form,
Here we should mention that the definitions,
bring us back to the principle of wave-particle duality, which we earlier saw in this document, in the form of the following equations,
where m is the mass of a material object, and μ is the mass of the wave ‘accompanying’ that object.
But here the notion of the brachistochrone of mass Mn, (at some state n), and the mass of the brachistochrone μn per wavelength λn of the reference photon, makes such a principle much clearer: The wave of mass μn which accompanies the object of mass m0 is associated with the wavelength λn of the reference photon (thus the mass μn refers to the mass of the wave, and not to the inertial mass m0 of the object), while the same mass μn, as a sub-division of the total mass Mn of the brachistochrone, is not the mass of a photon.
Now a similar division of the brachistochrone can be made with respect to Planck length lP, instead of the wavelength λ of the reference photon, if Planck length lP is used as a reference unit of length.
Thus in addition to the formulas
which give the number of photons Nn which fit in the length of the brachistochrone L0 at some state or harmonic n, we may suppose that the distance L0 is composed of a number NP of Planck lengths lP. Since the distance L0 is supposed to be fixed, the number NP will be constant, independently of the state n, since Planck length is fixed. Thus, we have
This way we can add another term in the energy equation, referring to the number NP, as follows. At the first state, n=1, it will be
where mP is Planck mass.
Thus, at any state n, it will be
This way we have a term in the energy equation referring to Planck length.
Before writing down the full energy equation, including all terms, we will make a third step, in order to include in the energy equation a term which will refer to the graviton mass, which we may call mg. As we previously did with the numbers N and NP, referring to the number of photons, or Planck lengths, respectively, which fit in the distance L0, we may introduce a number N΄, which will refer to the number of gravitons of mass mg which compose the mass Mn of the brachistochrone, at some state n.
Thus if N0΄ is the number of gravitons which compose the mass M0 of the brachistochrone at the first state,
then, if Nn΄ is the number of gravitons which compose the mass Mn of the brachistochrone at some state n, it will be
This way we have the following additional energy term, with respect to the number N΄ of gravitons of mass mg,
where λg is the graviton’s wavelength.
Gathering now together all the terms, we have for the numbers n, N, NP, and N΄, that
so that the energy E0 at the first state will be
and the energy En, at any state n, will be
while the corresponding energy per wavelength will be,
Here are some relationships which we can derive from the energy equation of the brachistochrone,
with respect to the masses m0, μn, and Mn,
or with respect to the speeds vn and c,
Thus we see, among other things, that the speed vn of the object and the speed of light c can be more generally defined by the previous formulas.
Another observation is that the state of the brachistochrone (referring to the number N of photons) is directly related to the harmonic n (referring to the excited state of the photon),
Also, the energy of the brachistochrone En at any harmonic n, is a multiple squared of the energy E0 at the first harmonic,
This gives us the freedom to use the terms ‘state,’ or ‘harmonic,’ of the brachistochrone interchangeably, keeping in mind the distinction between the numbers n and N, wherever this is necessary.
Notes:
We have already used the assumption that if the speed v0 of the object at the first state, n=1, is set equal to the speed of light c, then from the formulas,
we take the simpler result,
Another possible way to simplify the energy equation is to assume that as the harmonic n increases, the number of photons Nn which compose the length L0 approaches the number n,
By equating the length L0 of the brachistochrone to the wavelength λ0 of the reference photon, the number of photons N will always be equal to their harmonic n, so that we take simpler relationships, such as
If we additionally equate the speed v0 to the speed of light c,
then we take even simpler expressions,
However, by doing this, from the energy equation we also take that,
so that we take as a result that the wavelength λ0 of the reference photon will be equal to Planck length lP, while the mass m0 of the moving object will be equal to Planck mass mP.
Thus, although by equating different parameters we may take simple results, oversimplifications may result in our losing the physical meaning of the problem.
Finally we may also note some aspects with respect to the term in the energy equation associated with Planck energy. By dividing the brachistochrone into Planck lengths lP (instead of wavelengths λ0 of some photon of reference), we take for the energy per wavelength, that
so that the energy ε0 per wavelength λ0 will be identical to Planck energy εP.
In that sense the energy E0 may be considered the total energy (for all Planck lengths lP),
where, among others, we have the following relationships,
An application of such a substitution will be further explored later on.
Still, if the total energy En, for all harmonics n, is n2 times greater than the energy E0 at the first state, n=1,
then we may assume photon wavelengths λn much shorter than Planck length lP.
Therefore, in addition to the meaning of photons with macroscopic wavelengths, as we earlier saw, λ0≈L0, λn<<L0, we have also to consider the consequences of having photons with wavelengths smaller than Planck length, λ0≈lP, λn<<lP.
However, in such cases, the problem may not lie on the theoretically infinite possibilities, but on the practical limits of measurement.
But here the notion of the brachistochrone of mass Mn, (at some state n), and the mass of the brachistochrone μn per wavelength λn of the reference photon, makes such a principle much clearer: The wave of mass μn which accompanies the object of mass m0 is associated with the wavelength λn of the reference photon (thus the mass μn refers to the mass of the wave, and not to the inertial mass m0 of the object), while the same mass μn, as a sub-division of the total mass Mn of the brachistochrone, is not the mass of a photon.
Now a similar division of the brachistochrone can be made with respect to Planck length lP, instead of the wavelength λ of the reference photon, if Planck length lP is used as a reference unit of length.
Thus in addition to the formulas
Thus, at any state n, it will be
Before writing down the full energy equation, including all terms, we will make a third step, in order to include in the energy equation a term which will refer to the graviton mass, which we may call mg. As we previously did with the numbers N and NP, referring to the number of photons, or Planck lengths, respectively, which fit in the distance L0, we may introduce a number N΄, which will refer to the number of gravitons of mass mg which compose the mass Mn of the brachistochrone, at some state n.
Thus if N0΄ is the number of gravitons which compose the mass M0 of the brachistochrone at the first state,
Gathering now together all the terms, we have for the numbers n, N, NP, and N΄, that
Another observation is that the state of the brachistochrone (referring to the number N of photons) is directly related to the harmonic n (referring to the excited state of the photon),
Notes:
We have already used the assumption that if the speed v0 of the object at the first state, n=1, is set equal to the speed of light c, then from the formulas,
so that we take as a result that the wavelength λ0 of the reference photon will be equal to Planck length lP, while the mass m0 of the moving object will be equal to Planck mass mP.
Thus, although by equating different parameters we may take simple results, oversimplifications may result in our losing the physical meaning of the problem.
Finally we may also note some aspects with respect to the term in the energy equation associated with Planck energy. By dividing the brachistochrone into Planck lengths lP (instead of wavelengths λ0 of some photon of reference), we take for the energy per wavelength, that
In that sense the energy E0 may be considered the total energy (for all Planck lengths lP),
Still, if the total energy En, for all harmonics n, is n2 times greater than the energy E0 at the first state, n=1,
Therefore, in addition to the meaning of photons with macroscopic wavelengths, as we earlier saw, λ0≈L0, λn<<L0, we have also to consider the consequences of having photons with wavelengths smaller than Planck length, λ0≈lP, λn<<lP.
However, in such cases, the problem may not lie on the theoretically infinite possibilities, but on the practical limits of measurement.





















































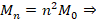















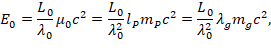








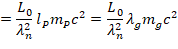








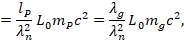































































No comments:
Post a Comment