Image: Representation of a brachistochrone S of radius R and of mass M, together with a reference photon of wavelength λ. The mass of the brachistochrone is seen as concentrated on the focus (black dot), and produces a uniform acceleration g.
In this picture, the wavelength λ of the reference photon is half a wavelength. The photon is represented as a standing wave. We may also note that the wavelength of the photon can be seen as a small brachistochrone of size λ/2, within the larger brachistochrone S.
Furthermore, the mass m represents an object travelling on the brachistochrone S. The mass M is the mass of the brachistochrone, and it is considered to be concentrated on the focus of the brachistochrone (at point M). The acceleration g is supposed to be uniform, covering the whole area of the brachistochrone.
This is a first approach to the energy of the brachistochrone, the successive terms of which we have already seen in the previous couple of sections,
In that form, the above quantities represent total energies, at some state of the brachistochrone n, although the state is not explicitly noted here.
The first term can also be written as,
where
is the common gravitational energy.
The second term is Einstein energy of the brachistochrone (E=mc2). But here the distinction was made between the mass of the object m0, and the mass of the brachistochrone MB.
The third term is the common kinetic energy of an object of mass m0, if its final speed if v. We can assume that the total kinetic energy mv2 is twice the average kinetic energy (1/2mv2), so that we drop the ½ factor.
The fourth term refers to the Planck energy of a photon of wavelength λ,
so that the total Planck energy stored in the distance LB will be
where the quantity
will be the number of photons of wavelength λ which compose the distance LB (at some state of the brachistochrone).
Here is a comparison between some of the pairs,
This is an indication that the speed v of an object moving on the brachistochrone can exceed the speed c of light, if the inertial mass m0 of the moving object is smaller than the mass of the brachistochrone MB,

Expressions for the masses m0 and MB can also be taken from the following pairs,
From these expressions we take back the previous ratio,
From the same energy pairs, we may also take expressions for the speed v of the moving object, and for the speed of light c,
Thus a formula of the form
will be a special case, if the inertial mass of the object moving on the brachistochrone is comparable to the mass of the brachistochrone, m0≈MB.
The energy EB can also be expressed with respect to the time TB of the brachistochrone,
where
where rP is Planck radius.
Also, for the period τ of the reference photon, we have that
The last formula shows the dependence of the period τ of the reference photon on the speed v of the moving object.
Notes:
The next to last formula, referring to the time TB of the brachistochrone, has the advantage of including all the fundamental constants: the speed of light c of relativity, Planck constant h of quantum mechanics, and Newton’s constant G of gravity.
The same formula can also be solved for the radius of the brachistochrone RB,
If in this formula we equate the two times, the time of the brachistochrone TB, and the period of the reference photon τ, we take the formula for Planck length lP (here Planck radius rP),
On the other hand, if we equate the period of the reference photon τ to Planck time tP,
(where a factor of 2π was added here for reasons of compatibility),
we take
And because, more generally, as we have already seen,
we have also to conclude that if the period τ of the reference photon is equal to Planck time tP, then the speed v of the moving object will be the speed of light c.
Consequently if the speed v of the objet exceeds the speed of light c, then the period τ of the reference photon will be smaller than Planck time tP. If this is true, then the energy equation of the brachistochrone, in addition to bringing together the aspects of the macrocosm with those of the microcosm, it also expands the limits.
However if we don’t have a way to distinguish between the different parameters, such as the lengths LB, λ and lP, or the corresponding times TB, τ, and tP, or the different masses MB and m0, which appear in the system of the brachistochrone, we won’t be able to make the necessary reductions, or to find for the same quantities a physical meaning.
In this picture, the wavelength λ of the reference photon is half a wavelength. The photon is represented as a standing wave. We may also note that the wavelength of the photon can be seen as a small brachistochrone of size λ/2, within the larger brachistochrone S.
Furthermore, the mass m represents an object travelling on the brachistochrone S. The mass M is the mass of the brachistochrone, and it is considered to be concentrated on the focus of the brachistochrone (at point M). The acceleration g is supposed to be uniform, covering the whole area of the brachistochrone.
This is a first approach to the energy of the brachistochrone, the successive terms of which we have already seen in the previous couple of sections,
The first term can also be written as,
The second term is Einstein energy of the brachistochrone (E=mc2). But here the distinction was made between the mass of the object m0, and the mass of the brachistochrone MB.
The third term is the common kinetic energy of an object of mass m0, if its final speed if v. We can assume that the total kinetic energy mv2 is twice the average kinetic energy (1/2mv2), so that we drop the ½ factor.
The fourth term refers to the Planck energy of a photon of wavelength λ,
Here is a comparison between some of the pairs,

The energy EB can also be expressed with respect to the time TB of the brachistochrone,
Solving for the time of the brachistochrone TB, we take,
Also, for the period τ of the reference photon, we have that
Notes:
The next to last formula, referring to the time TB of the brachistochrone, has the advantage of including all the fundamental constants: the speed of light c of relativity, Planck constant h of quantum mechanics, and Newton’s constant G of gravity.
The same formula can also be solved for the radius of the brachistochrone RB,
we take
Consequently if the speed v of the objet exceeds the speed of light c, then the period τ of the reference photon will be smaller than Planck time tP. If this is true, then the energy equation of the brachistochrone, in addition to bringing together the aspects of the macrocosm with those of the microcosm, it also expands the limits.
However if we don’t have a way to distinguish between the different parameters, such as the lengths LB, λ and lP, or the corresponding times TB, τ, and tP, or the different masses MB and m0, which appear in the system of the brachistochrone, we won’t be able to make the necessary reductions, or to find for the same quantities a physical meaning.













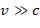















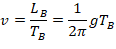





















No comments:
Post a Comment