Up till now we have seen two examples of motion, that of the ship- in- the- sea, and that of the rocket-in-space. The equations of motion are respectively
If we combine the two equations (without repeating the term ma) we take
This is the equation of the damped harmonic oscillator. It includes both a harmonic term (the elastic force Fel=ky), and a damping term (the damping force Fd=bv).
Rewriting the equation of motion as,
we can identify the quantity γ with the damping factor (so that we may call b the damping constant, and γ the damping factor). The quantity ω0 is the angular frequency of the simple harmonic oscillator (without damping).
Here we will assume a possible solution for the equation of motion of the damped harmonic oscillator, in the following form,
where ω΄ is the angular frequency of the damped oscillator (different from the angular frequency ω0), while φ is the phase, and its value depends on the boundary conditions.
For the speed v and the acceleration a, we will have
The last equation is a condition which satisfies the given solution.
The graph of this solution is the following one,
The black dotted line in the previous graph is the exponential envelope of the amplitude (red line). Thus the amplitude y(t) oscillates because of the cosine term, and also decays because of the exponential term.
With respect to the energy of the system, the elastic energy Eel and the kinetic energy Ek will be commonly given by the following expressions,
so that
The expression for the kinetic energy Ek is somewhat complicated. Choosing however some initial condition,
we take simpler expressions for the elastic energy Eel and the kinetic energy Ek (in the form of the total energy).
Another boundary condition can be taken at some time t equal to the period T of the oscillator,
so that at the conclusion of a cycle, t=T, for the elastic energy Eel, and the kinetic energy Ek, we have
The mechanical energy Em of the system at times t=0 and t=T will respectively be,
Thus at the conclusion of one cycle the change of the mechanical energy will be,
Here the total mechanical energy E0≡Em(t=0) includes both an elastic term ½mω02y02, and a damping term ½ m(γ2/4)y02.
The final boundary condition at time t=T also defines the mechanical energy Em of the oscillator at any time t. Setting for example t=νT, where ν is a positive integer, we have that
so that the expression for the mechanical energy can be written as
The same solution for the mechanical energy can be taken in a straightforward way, if we consider the rate of change of the mechanical energy. Multiplying each term in the equation of motion by v, we take
The first term is the rate of change of the mechanical energy,
Therefore the second term can be identified with the rate of change of the damping energy,
The last term can be compared to the kinetic energy,
We may assume that the average rate of change of the kinetic energy is half the rate of change of the mechanical energy. This is based on the simple harmonic oscillator (without damping), where for the energies
we have the following average values,
That the average value of sin2ω0t, or of cos20t, is ½ will be calculated later on.
Thus the previous equation takes the form,
Thus we have the following equations, with respect to the energy of the damped harmonic oscillator,
This result is similar to the one we took in the rocket- in- space example, with the exception of the factor 2 in the exponential, which here is absent because of the contribution of the harmonic (the elastic) term ky.
The term μ0c2, which was included in the last expression for the total energy E0 of the oscillator, refers to the mass μ0 of the oscillator, not to the mass m of the object (‘hanging’ on the ‘spring’ of the oscillator).
Rewriting the equation of motion as,
Here we will assume a possible solution for the equation of motion of the damped harmonic oscillator, in the following form,
For the speed v and the acceleration a, we will have
Substituting this solution into the equation of motion, we take
The graph of this solution is the following one,
The black dotted line in the previous graph is the exponential envelope of the amplitude (red line). Thus the amplitude y(t) oscillates because of the cosine term, and also decays because of the exponential term.
With respect to the energy of the system, the elastic energy Eel and the kinetic energy Ek will be commonly given by the following expressions,
Another boundary condition can be taken at some time t equal to the period T of the oscillator,
The final boundary condition at time t=T also defines the mechanical energy Em of the oscillator at any time t. Setting for example t=νT, where ν is a positive integer, we have that
Thus the previous equation takes the form,
The term μ0c2, which was included in the last expression for the total energy E0 of the oscillator, refers to the mass μ0 of the oscillator, not to the mass m of the object (‘hanging’ on the ‘spring’ of the oscillator).



























































































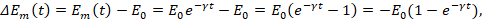

No comments:
Post a Comment