In the previous section we arrived at an equation of the form,
which connects the energy EB (or En) of the brachistochrone to its informational context IB (or In).
This connection is made possible by considering the states n of the system, so that the energy En at the n-th state will be n2 times greater than the energy E0 at the ground state (n=1),
Presumably the constant 𝒞 is equal to the natural logarithm of the total energy En at the state n.
We can show that the previous equation is related to the energy in the exponential form,
This energy is associated with the damped harmonic oscillator, and we have already shown that the brachistochrone is an oscillator, so that the previous equation also applies to the energy of the brachistochrone.
The states n of the system can appear by setting
As the number n increases, the exponential in this equation goes to 1/n2 (or even to 1/n for large enough n), so that
Using a negative exponential, the total energy is in fact E0. Otherwise, if we use a positive exponential the total energy will be E(n),
Therefore either of the last two exponential forms for the energy at large n,
are similar to the linear form,
Here we will see how the constant 𝒞 emerges in the previous equations. We can begin with the equation of motion of the damped harmonic oscillator,
which we can rewrite as
and multiply each side by v (as we have already done elsewhere), so that
The left hand side is the change of the mechanical energy, which we can simply call E, so that
Comparing the rate of change of the energy E, to the energy itself, we have
where γ is the damping factor.
If the condition of critical damping is applied, as we have already seen, the kinetic energy is equal to the elastic energy, so that the mechanical energy will be twice as much (mv2, instead of ½mv2).
Solving the last differential equation, we have
The constant of integration which appears in the next to last equation
represents in fact the total energy E0 of the system, for all states γt=n, and since it is equal to the logarithm of the energy, it is a dimensionless quantity.
Formally, the information I of the system is given as the logarithm of the states,
Here however, for simplicity, we will suppose that the information can be defined as the logarithm of the energy,
In that sense, the constant 𝒞,
will stand for the total amount of information available to the system.
This is why I call this constant 𝒞 for Consciousness.
Thus the equation
can also be written in the equivalent form
A more compact form can be taken by using the following substitution,
so that the equation for the total energy, including the factor Γ, can be written in the equivalent forms,
Since the factor Γ is related to how fast information is absorbed, I will call the factor Γ, Factor of Free Will.
Incidentally, there is another reason why the letter Γ was used for this factor. Using the substitution,
we can rewrite the factor Γ as a function of the speed v,
so that the energy with respect to the speed v will be,
Comparing the equation for the energy in the latter form to the relativistic energy,
we see that while in relativity the energy becomes infinite at the speed of light, the energy with respect to the factor Γ is bounded for all speeds. This happens because while the Lorentz factor γL(v) goes to infinity as the speed v approaches the speed of light, v=c=1, c=1, the factor Γ(v) goes to infinity only when the speed v becomes infinite.
A final note can be made with respect to the difference in the energy,
The difference ΔE in the energy can be identified with the kinetic energy (which here is called K), in the sense that the total initial energy E0 is transformed into the motion of an object.
We may call the process by which the total potential energy E0 of the system is transformed into the kinetic energy K of an object, ‘Displacement of Consciousness.’
In the epilogue some statements will be made about how the available energy, in the form of implicit information, transforms into the kinetic energy of a material object moving in spacetime, if this object is Consciousness itself.
This connection is made possible by considering the states n of the system, so that the energy En at the n-th state will be n2 times greater than the energy E0 at the ground state (n=1),
We can show that the previous equation is related to the energy in the exponential form,
The states n of the system can appear by setting
If the condition of critical damping is applied, as we have already seen, the kinetic energy is equal to the elastic energy, so that the mechanical energy will be twice as much (mv2, instead of ½mv2).
Solving the last differential equation, we have
Formally, the information I of the system is given as the logarithm of the states,
This is why I call this constant 𝒞 for Consciousness.
Thus the equation
Incidentally, there is another reason why the letter Γ was used for this factor. Using the substitution,
A final note can be made with respect to the difference in the energy,
We may call the process by which the total potential energy E0 of the system is transformed into the kinetic energy K of an object, ‘Displacement of Consciousness.’
In the epilogue some statements will be made about how the available energy, in the form of implicit information, transforms into the kinetic energy of a material object moving in spacetime, if this object is Consciousness itself.


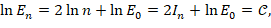


























































No comments:
Post a Comment