Contents
Basic principles
Appendix 1
Energy in relativistic damping
Appendix 2
The nature of spacetime
Basic principles
Combining this formula with that of Compton’s wavelength
we take
This can also be seen if we use the formula for Planck energy,
Thus we have
It is illustrative to make a comparison with Newton’s second law
The next to last equation of the forces has the following simple solutions
where we took the measure of these quantities, ignoring thus any negative sign (the rate β is in fact negative because the mass μ of the wave decreases).
From the previous equation we can take an expression for the damping factor γ (while β will be the damping constant)
What is significant is that the mass μ of spacetime is not a constant. Thus we can write
The damping factor γ plays a central role in the whole analysis
The next step is to define the energy equation of the wave-object system
We may note that the formulas
give us respectively a first and second order relationship between the masses and the speeds.
Energy in relativistic damping
The functions depicted in the previous graph (red and green lines) are respectively
In order to express this energy as a function of the speed v, we set
This substitution is justified by the expression for the damping factor
But the total energy E0 of spacetime will all be transformed into the kinetic energy of the moving object only if the speed of the object is much greater than the speed of light,
If we compare the previous energy to the relativistic kinetic energy, we have
The nature of spacetime
Based on such coincidences, we can also consider another one

Therefore speeds much faster than light are possible.
[https://archive.org/details/CrossingTheBrachistochrone_201804]
© 2018 Chris C. Tselentis
Last updated: 4/18/2018
Mailto: christselentis@gmail.com
Basic principles
Appendix 1
Energy in relativistic damping
Appendix 2
The nature of spacetime
Basic principles
This is a brief exposition of some basic notions concerning the principle of wave-particle duality, and the possibility of faster than light travel. The title of this document refers to the damping factor which appears in the related formulas, and by which a correction to the corresponding relativistic expressions can be made.
Classically the momentum, which we may call pm, of a material object of mass m, moving at a speed v is
On the other hand, the momentum, which we may call pμ, of a wave of wavelength λ is given by de Broglie’s formula
The quantity μ describes the mass of the wave, not the inertial mass m of the material object. This wave is associated with the oscillations of the medium (spacetime) in which the object moves. Therefore spacetime is not empty, but it contains some mass μ.
This can also be seen if we use the formula for Planck energy,
The last term gives Einstein’s formula of mass-energy equivalence. Here however the important distinction is made between the mass m of an object and the mass μ of spacetime.
Assuming that the total momentum p0 of the wave- particle (or spacetime- material object) system is conserved, we have
The related forces are taken if we differentiate the momenta with respect to time. Here however a distinction will be made between the coordinate time t of an observer on the moving object, and the period T of the wave on which the object moves.
Incidentally a straightforward relationship between the coordinate displacement x of the object and the displacement λ of the wave can be given by the following formulas
While a is the common acceleration of an object of mass m (the inertial mass is always a constant), β is the damping constant (μ is not a constant), and c is the speed of the wave (presumably the speed of light, which is constant). The quantity ρ is the density of the wave.
It is illustrative to make a comparison with Newton’s second law
The problem here is that the mass m is treated both as a constant and as a changing quantity. This problem is solved by separating the inertial mass m of the object from the mass μ of spacetime. The mass μ can also be seen as the mass of the fuel of the object. But if we imagine that the object (e.g. a spaceship) can collect its fuel directly from space, instead of storing them, then the fuel will be all the available energy (or the mass μ equivalent) stored in a region of spacetime.
The next to last equation of the forces has the following simple solutions
From the previous equation we can take an expression for the damping factor γ (while β will be the damping constant)
The quantities μ0 and T0 refer to the total (initial) mass and period of the wave, while v0 refers to the total (final) speed of the object.
What is significant is that the mass μ of spacetime is not a constant. Thus we can write
Therefore it is supposed that the mass of spacetime reduces exponentially with time (as it is utilized by the moving object).
The damping factor γ plays a central role in the whole analysis
The energy Em≡Ek of the object is the common kinetic energy. The energy Eμ≡Ed is the energy of the wave, and can be also called damping energy.
We may note that the formulas
A final step is to find the rate of change of the energies with respect to the time t (the rate of change of the damping energy Ed can be expressed either with respect to the coordinate time t or with respect to the period T of the wave)
This is the energy of the system. The damping energy Ed of the wave of spacetime reduces exponentially, as it is transformed into the kinetic energy Ek of the object moving in spacetime.
A fundamental consequence of this analysis and the related equations is that the object can move faster than light. From the total energy E0 of the system we have
Therefore the final speed v0 of the object can be greater than the speed of light c, as long as its mass m is smaller than the mass μ0 which is stored in a region of spacetime. If the object reaches the speed of light, its kinetic energy Ek will simply be 1/2mc2. But the total energy E0 of ‘fuel’ (of the region of spacetime where the object is moving) will still be μ0c2.
Energy in relativistic damping
Comparison between the relativistic expression for the kinetic energy (red line), and the correction function (green line) for the kinetic energy where damping is included.
The functions depicted in the previous graph (red and green lines) are respectively
As a first note, a comparison with the energy in relativity will be made. In relativity the energy is given by the formula
Here m is the relativistic mass, while m0 is the rest mass. Correspondingly, E0 is the rest energy. The quantity γL is the Lorentz factor. The relativistic kinetic energy is given as the difference
If the speed of the moving object is sufficiently small then the relativistic kinetic energy is reduced to the classical expression for the kinetic energy
However if the speed of the object approaches the speed of light, the relativistic kinetic energy goes to infinity
It is assumed that as the speed of the moving object approaches the speed of light, its mass becomes infinite, so that the object cannot exceed the speed of light. However as the mass of the object becomes infinite, its kinetic energy will also be infinite. This is because the Lorentz factor goes to infinity at the speed of light. Therefore the relativistic energy cannot be defined at speeds equal to or greater than the speed of light.
Now in order to make the comparison between the kinetic energy in relativity and the kinetic energy in relativistic damping, we have to express the later energy as a function of the speed v
where we have explicitly noted the damping factor γ as γd, so that it is not confused with the Lorentz factor γL.
In order to express this energy as a function of the speed v, we set
The meaning of the previous substitution is that at some time interval Δt=t equal to the difference ΔT=T0-T, where T0 is the initial period and T is the final period of the wave. If the object has reached the speed of light, v=c, then the kinetic energy of the object will have increased by a factor of e
The previous equations are in fact a first order approximation. This can be seen from the pairs
Taking the second order approximation (using the second of the previous pairs), we have
This function for the kinetic energy Ek(v) is depicted in the previous graph (green curve).
If the speed of the moving object is sufficiently smaller than the speed of light, we take back the relativistic expression for the kinetic energy (red curve in the previous graph)
If the moving object approaches the speed of light, its kinetic energy increases by a factor of e-1/2
But the kinetic energy in relativistic damping can still be defined if the speed of the object is greater than the speed of light
In such a way we can have speeds (infinitely) greater than the speed of light, even if the best energy efficiency is at the speed of light (the derivative of the kinetic energy is zero at the speed of light), while the total energy is always bounded (theoretically all the energy available in the universe). This is possible because spacetime is treated as a real entity with some total mass μ0, different from the inertial mass m of any object moving in spacetime.
The nature of spacetime
As a second note, the ultimate question is about the nature of spacetime and its oscillations. However the notion of Planck energy may refer to any kind of medium. If we know the wavelength λ of the oscillations of the medium, we can also estimate its mass or energy
This is in fact the energy per wavelength λ of the oscillations. For a macroscopic distance L to be traveled, if this distance is composed of N wavelengths λ, the total energy will be
Simpler, if we divide the distance L into Planck lengths lP (assuming that this is the smallest possible wavelength), so that the distance L is composed of n Planck lengths, then the energy will be
Ιt doesn’t really matter if we call the total energy E ‘Planck energy’ or ‘gravitational energy,’ or whether we call space ‘quantum vacuum,’ or ‘spacetime,’ as long as we know how much the total energy is.
The equivalence between the various forms of energy, which goes beyond the principle of wave- particle duality, can be shown for example if we include the mass mg and wavelength λg of the graviton in the previous energy equation
Considering these parameters of the problem, some interesting coincidences of universal nature arise. If MU and RU is the mass and radius of the observable universe respectively, and we call ρU the linear density of the observable universe, then we have
The last equation relates the ratios of the various fundamental parameters (presumably constants) of the problem to each other, and expresses mathematically the numerical coincidence between the same parameters. In fact the mass MU of the observable universe was estimated here so that the ratio of the mass MU over the radius RU of the observable universe coincides with the ratio of Planck mass mP over Planck radius rP (as was previously defined in relation to Planck length lP). We also see that the product of the linear density ρU of the observable universe by Newton’s gravitational constant G is equal to the speed of light c squared.
Based on such coincidences, we can also consider another one
The acceleration ℊ which appears in the last equation is a uniform acceleration throughout the universe, and if we accept the numerical coincidence between the graviton’s mass mg and Planck’s constant h (transformed into light units), so that the graviton’s wavelength λg is exactly 1ly, then the value of ℊ is indeed 1ly/y2.
The previous calculations were made in brief, but the replacements are straightforward. The numerical coincidences involved portray the equivalence between the various forms of energy which may appear in the problem, so that we can ultimately link them to the kinetic energy of a (material) object moving in space (the medium)

The previous equations refer to total energies, thus also to the total (final) speed v. According to these equations, in order for an object (e.g. a spaceship), traveling in spacetime along a distance L, to reach the speed of light, it is sufficient to consume a mass M, found along the same distance L, equal to ½ its own inertial mass m.
Assuming for the spaceship a mass m equal to that of a modern supercarrier, if the distance L to be traveled is the radius RU of the whole observable universe, then the spaceship’s final speed will be
For a more detailed analysis of this subject, on can see another document of mine, ‘Crossing the brachistochrone,’ on the following link:
[https://archive.org/details/CrossingTheBrachistochrone_201804]
© 2018 Chris C. Tselentis
Last updated: 4/18/2018
Mailto: christselentis@gmail.com







































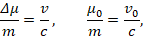























































































































No comments:
Post a Comment