Contents
Prologue
1. About this document
Part 1: Grasping the scales
1.1 Size and age of the universe
1.2 Age and structure of the Milky Way
1.3 Methuselah stars
1.4 The expanding universe
1.5 Our location in the universe
1.6 The universe as a living organism
Part 2: Drake’s equation
2.1 Aspects of Drake's equation
2.2 Number of stars
2.2.1 Rate of stars
2.2.2 Lifespan of stars
2.2.3 Habitability of red dwarf systems
2.2.4 Populations of stars
2.2.5 Peak population of MS stars
2.2.6 Generations of civilizations
2.3 Number of exoplanets
2.3.1 Earth analog
2.3.2 Habitable zone
2.3.3 Habitability outside the CHZ
2.4 Life on exoplanets
2.4.1 Abiogenesis
2.4.2 The problem of homochirality
2.4.3 Life is abundant
2.4.4 Selective destruction
2.5 Intelligent life
2.5.1 Defining intelligence
2.5.2 Intelligent life is unique
2.5.3 Possibility of communication
2.5.5 Timeline of intelligent life
2.6 The number L
2.6.1 Life expectancy
2.6.2 Extinction event
2.6.3 Our closest neighbors
2.7 Number of civilizations
Part 3: Expanding Drake’s equation
3.1 Exponential vs logistic growth
3.2 Statistical Drake’s equation
3.3 The normal distribution
3.4 Distribution of MS stars
3.5 Kardashev’s scale
3.6 Distribution of civilizations
3.7 ETIQ
3.8 Peak population
Part 4: Fermi’s paradox
4.1 About Fermi’s paradox
4.2 The horizon problem
4.3 A thought experiment
4.4 Information paradox
4.5 Technological event horizons
4.6 Entropy and invisibility
4.7 Cosmological exclusion principle
4.8 The mediocrity principle
4.9 Speciation vs colonization
Epilogue
5.1 So where are they?
5.2 The anthropic principle
5.3 Principle of non-intervention
5.4 Dyson spheres
5.5 UFO’s as psychic phenomena
5.6 To Alpha Centauri and beyond
Appendix
6.1 Grasping the scales once more…
Prologue
1. About this document
Part 1: Grasping the scales
1.1 Size and age of the universe
1.2 Age and structure of the Milky Way
1.3 Methuselah stars
1.4 The expanding universe
1.5 Our location in the universe
1.6 The universe as a living organism
Part 2: Drake’s equation
2.1 Aspects of Drake's equation
2.2 Number of stars
2.2.1 Rate of stars
2.2.2 Lifespan of stars
2.2.3 Habitability of red dwarf systems
2.2.4 Populations of stars
2.2.5 Peak population of MS stars
2.2.6 Generations of civilizations
2.3 Number of exoplanets
2.3.1 Earth analog
2.3.2 Habitable zone
2.3.3 Habitability outside the CHZ
2.4 Life on exoplanets
2.4.1 Abiogenesis
2.4.2 The problem of homochirality
2.4.3 Life is abundant
2.4.4 Selective destruction
2.5 Intelligent life
2.5.1 Defining intelligence
2.5.2 Intelligent life is unique
2.5.3 Possibility of communication
2.5.5 Timeline of intelligent life
2.6 The number L
2.6.1 Life expectancy
2.6.2 Extinction event
2.6.3 Our closest neighbors
2.7 Number of civilizations
Part 3: Expanding Drake’s equation
3.1 Exponential vs logistic growth
3.2 Statistical Drake’s equation
3.3 The normal distribution
3.4 Distribution of MS stars
3.5 Kardashev’s scale
3.6 Distribution of civilizations
3.7 ETIQ
3.8 Peak population
Part 4: Fermi’s paradox
4.1 About Fermi’s paradox
4.2 The horizon problem
4.3 A thought experiment
4.4 Information paradox
4.5 Technological event horizons
4.6 Entropy and invisibility
4.7 Cosmological exclusion principle
4.8 The mediocrity principle
4.9 Speciation vs colonization
Epilogue
5.1 So where are they?
5.2 The anthropic principle
5.3 Principle of non-intervention
5.4 Dyson spheres
5.5 UFO’s as psychic phenomena
5.6 To Alpha Centauri and beyond
Appendix
6.1 Grasping the scales once more…
1. About this document
Drake’s equation has been a great inspiration of mine. On one hand, it is the straightforward and simple way by which this equation estimates the possible number of extraterrestrial civilizations. On the other hand, it is the analysis of the parameters of the equation which makes one begin a journey into the universe.
It is estimated that there are 100 billion stars in the Milky Way, and that there are probably 100 billion galaxies in the universe. But even if the universe is full of galaxies, and the galaxies are full of stars, while most of the stars may have planets, on some of which life may have evolved, so that there could be a considerable number of other civilizations out there, the distances are so great that, in addition to our limited means of communication at the moment, the chance of finding and contacting an extraterrestrial civilization like our own is little.
This is not to say that life is rare in the universe. On the contrary abiogenesis suggests that it takes a few basic chemical elements for life to begin with. However the evolution of primitive life to the level of an intelligent species is another matter. Thus it is possible that, although life in the form of microbes is quite abundant in the universe, advanced life in the form of intelligent lifeforms may be rather sparse and unique, so that, given the great distances, the possibility of communication is remote.
This brings us to Fermi’s paradox: Even if the density of extraterrestrial civilizations in the universe is low (there may be a considerable number of other civilizations, but the distance between civilizations is also great), some of those civilizations should have evolved sufficiently enough to have discovered interstellar travel, and to have visited other worlds like ours. So where are they? Thus the paradox.
A possible answer to this paradox is I believe two-fold. On one hand, we have the fact that it will be difficult for two less advanced civilizations in interstellar travel and communication, like our own, to communicate or visit each other. On the other hand, a highly advanced civilization, capable of sophisticated communication, and knowing ways of interstellar travel which are unimaginable to us at present, will practically be undetectable by a less advanced civilization like ours.
Such a civilization will have passed beyond its own technological singularity, thus there will be a ‘technological event horizon’ between them and us, and they would probably have adopted ways and states of existence beyond our own brain capacity and ability of perception. Thus even if they came we wouldn’t make out them more than ‘lights in the sky,’ offering about them explanations which we are already familiar with (e.g. weather balloons). On the other hand, if they made themselves apparent to us, they would likely cause a culture shock, since we are basically ill-prepared for the contact, and our reaction would mostly be irrational and violent.
In such a sense we may say that our own brain and nature have effectively invented a protective mechanism for the event of such a contact. This is what I call the ‘cosmological exclusion principle.’ On one hand, two primitive civilizations like our own, who destroy their environment and make war, would probably annihilate each other if they come in contact. Thus nature has provided for great interstellar distances, so that primitive civilizations is difficult to meet each other. On the other hand, a sufficiently advanced civilization, leaving a small technological imprint on its surroundings, and having plentiful resources at its disposal in order to prevent war, will avoid to interfere with less advanced civilizations, either because of the lack of motive, or because of the consequences. This is what I call ‘principle of non- intervention.’
Thus the important question is not ‘Where are they?’ Instead it is ‘What if they had come?’ The immatureness of our civilization, which naturally stems from our own ignorance of the Cosmos, is responsible both for the blind faith in aliens, as if they were self- evident Gods, as well as for the axiomatic rejection of their existence, because of the threat they would pose to our own social establishment.
Here however I would like to make the following suggestion. UFO sightings are usually accompanied by unexplained premonitions and strange sentiments. Since we have never really captured aliens or one of their machines (despite conspiracy theories), our experience and knowledge of them is purely psychological and unconscious. This is why I believe that, after having accepted at least the possibility of their existence, we should treat aliens or their flying machines, instead of material entities or tangible objects, as purely psychic phenomena. The natural process by which a species is gradually prepared on a psychological level to come in contact with an alien species can be called ‘preparation.’ This may explain the increasing number of UFO ‘sightings’ which occur nowadays.
According to the anthropic principle, we are fined-tuned with the universe so that we are able not only to understand the universe, but also to understand why we understand. If, according to the aforementioned cosmological exclusion principle, there is some kind of pre- established arrangement of the distances between civilizations, so that their mutual destruction is avoided, then there may also be some kind of providence for their communication or contact, so that two civilizations will meet each other only when they are both sufficiently advanced. Therefore the fine-tuning on the physical level, can also exist on the psychological and mental level.
Perhaps this didn’t happen when the Europeans arrived in the New World, as the more advanced Europeans subjugated or exterminated the less advanced native Indians. But in this example, although it is instructive, the scale is much smaller and narrower. Throughout human history there hasn’t been any contact or conflict between a ‘modern civilization’ and ‘ape-men.’ If we ever discover ‘stone people’ on another planet, our intention will probably be to avoid them, since machines work much better and cheaper than slaves, while any damage caused to them or to their planet will be inversely proportional to the sophistication of our machinery, and to our ability of extracting resources.
Recent observations suggest that the maximum rate of star production in the universe took place quite early, about 5 billion years after the Big Bang. If the life expectancy of a G-type star like our Sun is approximately 10 billion years, then the maximum number of stars like our Sun in the universe is occurring right now, about 15 billion years after the Big Bang. If we give a hiatus of 5 billion years for intelligent life to appear on a G-type star, as long as it took us to appear on our own solar system, then we should expect the peak population to take place in the universe about 20 billion years after the Big Bang, 5 billion years from now. This might explain the problem of ‘cosmic silence,’ since the number of other civilizations out there will still be low. However it is also probable that very few civilizations have had the time to advance at a high level, already visiting and terraforming exoplanetary systems.
Yet there seems to be enough empty space available for all in the universe. If right now just a couple out of 100 habitable planets has intelligent life as we know it, there will still be 98 unoccupied planets available for each of those intelligent lifeforms in the future. Breakthrough Starshot is the latest project planning a journey to Alpha Centauri. In the near future we may also discover the first exoplanetary civilization like our own, having thus answered the everlasting question whether we are alone in the universe. But perhaps the most important question is how we treat life on our own planet, as right now we are going through a sixth mass extinction of species.
1.1 Size and age of the universe
Drake’s equation has been a great inspiration of mine. On one hand, it is the straightforward and simple way by which this equation estimates the possible number of extraterrestrial civilizations. On the other hand, it is the analysis of the parameters of the equation which makes one begin a journey into the universe.
It is estimated that there are 100 billion stars in the Milky Way, and that there are probably 100 billion galaxies in the universe. But even if the universe is full of galaxies, and the galaxies are full of stars, while most of the stars may have planets, on some of which life may have evolved, so that there could be a considerable number of other civilizations out there, the distances are so great that, in addition to our limited means of communication at the moment, the chance of finding and contacting an extraterrestrial civilization like our own is little.
This is not to say that life is rare in the universe. On the contrary abiogenesis suggests that it takes a few basic chemical elements for life to begin with. However the evolution of primitive life to the level of an intelligent species is another matter. Thus it is possible that, although life in the form of microbes is quite abundant in the universe, advanced life in the form of intelligent lifeforms may be rather sparse and unique, so that, given the great distances, the possibility of communication is remote.
This brings us to Fermi’s paradox: Even if the density of extraterrestrial civilizations in the universe is low (there may be a considerable number of other civilizations, but the distance between civilizations is also great), some of those civilizations should have evolved sufficiently enough to have discovered interstellar travel, and to have visited other worlds like ours. So where are they? Thus the paradox.
A possible answer to this paradox is I believe two-fold. On one hand, we have the fact that it will be difficult for two less advanced civilizations in interstellar travel and communication, like our own, to communicate or visit each other. On the other hand, a highly advanced civilization, capable of sophisticated communication, and knowing ways of interstellar travel which are unimaginable to us at present, will practically be undetectable by a less advanced civilization like ours.
Such a civilization will have passed beyond its own technological singularity, thus there will be a ‘technological event horizon’ between them and us, and they would probably have adopted ways and states of existence beyond our own brain capacity and ability of perception. Thus even if they came we wouldn’t make out them more than ‘lights in the sky,’ offering about them explanations which we are already familiar with (e.g. weather balloons). On the other hand, if they made themselves apparent to us, they would likely cause a culture shock, since we are basically ill-prepared for the contact, and our reaction would mostly be irrational and violent.
In such a sense we may say that our own brain and nature have effectively invented a protective mechanism for the event of such a contact. This is what I call the ‘cosmological exclusion principle.’ On one hand, two primitive civilizations like our own, who destroy their environment and make war, would probably annihilate each other if they come in contact. Thus nature has provided for great interstellar distances, so that primitive civilizations is difficult to meet each other. On the other hand, a sufficiently advanced civilization, leaving a small technological imprint on its surroundings, and having plentiful resources at its disposal in order to prevent war, will avoid to interfere with less advanced civilizations, either because of the lack of motive, or because of the consequences. This is what I call ‘principle of non- intervention.’
Thus the important question is not ‘Where are they?’ Instead it is ‘What if they had come?’ The immatureness of our civilization, which naturally stems from our own ignorance of the Cosmos, is responsible both for the blind faith in aliens, as if they were self- evident Gods, as well as for the axiomatic rejection of their existence, because of the threat they would pose to our own social establishment.
Here however I would like to make the following suggestion. UFO sightings are usually accompanied by unexplained premonitions and strange sentiments. Since we have never really captured aliens or one of their machines (despite conspiracy theories), our experience and knowledge of them is purely psychological and unconscious. This is why I believe that, after having accepted at least the possibility of their existence, we should treat aliens or their flying machines, instead of material entities or tangible objects, as purely psychic phenomena. The natural process by which a species is gradually prepared on a psychological level to come in contact with an alien species can be called ‘preparation.’ This may explain the increasing number of UFO ‘sightings’ which occur nowadays.
According to the anthropic principle, we are fined-tuned with the universe so that we are able not only to understand the universe, but also to understand why we understand. If, according to the aforementioned cosmological exclusion principle, there is some kind of pre- established arrangement of the distances between civilizations, so that their mutual destruction is avoided, then there may also be some kind of providence for their communication or contact, so that two civilizations will meet each other only when they are both sufficiently advanced. Therefore the fine-tuning on the physical level, can also exist on the psychological and mental level.
Perhaps this didn’t happen when the Europeans arrived in the New World, as the more advanced Europeans subjugated or exterminated the less advanced native Indians. But in this example, although it is instructive, the scale is much smaller and narrower. Throughout human history there hasn’t been any contact or conflict between a ‘modern civilization’ and ‘ape-men.’ If we ever discover ‘stone people’ on another planet, our intention will probably be to avoid them, since machines work much better and cheaper than slaves, while any damage caused to them or to their planet will be inversely proportional to the sophistication of our machinery, and to our ability of extracting resources.
Recent observations suggest that the maximum rate of star production in the universe took place quite early, about 5 billion years after the Big Bang. If the life expectancy of a G-type star like our Sun is approximately 10 billion years, then the maximum number of stars like our Sun in the universe is occurring right now, about 15 billion years after the Big Bang. If we give a hiatus of 5 billion years for intelligent life to appear on a G-type star, as long as it took us to appear on our own solar system, then we should expect the peak population to take place in the universe about 20 billion years after the Big Bang, 5 billion years from now. This might explain the problem of ‘cosmic silence,’ since the number of other civilizations out there will still be low. However it is also probable that very few civilizations have had the time to advance at a high level, already visiting and terraforming exoplanetary systems.
Yet there seems to be enough empty space available for all in the universe. If right now just a couple out of 100 habitable planets has intelligent life as we know it, there will still be 98 unoccupied planets available for each of those intelligent lifeforms in the future. Breakthrough Starshot is the latest project planning a journey to Alpha Centauri. In the near future we may also discover the first exoplanetary civilization like our own, having thus answered the everlasting question whether we are alone in the universe. But perhaps the most important question is how we treat life on our own planet, as right now we are going through a sixth mass extinction of species.
It is important to notice that the age of the Milky Way galaxy is approximately equal to the age of the universe (although it seems that the thin disk of the Milky Way formed about 5 billion years after the Big Bang). Apart from the implications for modern cosmology (e.g. the universe seems to have formed by accretion from a pre-existing distribution of matter, instead of by the Big Bang), such an observation makes it possible that civilizations much older, thus also much more advanced, than our own may exist out there- the Sun formed 5 billion years ago, while the first MS (main sequence) stars may have formed 5 billion years earlier (when the thin disk of the Milky Way formed). The paradox which rises is that if the existed they would have already visited us. But this isn’t necessarily true if advanced civilizations avoid contact with less advanced or primitive civilizations like our own (compared to them). But let’s take a look at the huge cosmological scales first.
Visualization of the observable universe
[https://en.wikipedia.org/wiki/Observable_universe]
The distance of 93 billion light years in the previous picture refers to the ‘comoving’ distance due to the expansion of spacetime since the Big Bang. The horizon of the observable universe is 13.8 billion light years, and it is the distance light has travelled since the Big Bang, 13.8 billion years ago. Thus from our own perspective we can see astronomical objects which are as far as 13.8 billion light years away, but not further on. This might change when the nature of dark energy is understood (since the stretching of spacetime is related to dark energy).
Thus the universe is enormous. And this could be one of many universes in the multiverse. What exactly is meant by ‘multiverse’ is uncertain. But if another universe is connected to ours through a ‘wormhole’ (or through an extra dimension), so that we could travel ‘instantaneously’ to some place in that universe, then it could be more convenient to search for extraterrestrial life in that universe instead of our own solar neighborhood. This is an example of how relative the meaning of distance might be, not to mention the ambiguity of the term ‘extraterrestrial’ lifeform.
Our own universe has hundreds of billions of galaxies, and is estimated that there are hundreds of billions of stars in our galaxy alone:
It has been said that counting the stars in the Universe is like trying to count the number of sand grains on a beach on Earth. We might do that by measuring the surface area of the beach, and determining the average depth of the sand layer. If we count the number of grains in a small representative volume of sand, by multiplication we can estimate the number of grains on the whole beach.
For the Universe, the galaxies are our small representative volumes, and there are something like 1011 to 1012 stars in our Galaxy, and there are perhaps something like 1011 or 1012 galaxies. With this simple calculation you get something like 1022 to 1024 stars in the Universe. This is only a rough number, as obviously not all galaxies are the same, just like on a beach the depth of sand will not be the same in different places.
No one would try to count stars individually, instead we measure integrated quantities like the number and luminosity of galaxies. ESA’s infrared space observatory Herschel has made an important contribution by ‘counting’ galaxies in the infrared, and measuring their luminosity in this range- something never before attempted.
[http://www.esa.int/Our_Activities/Space_Science/Herschel/How_many_stars_are_there_in_the_Universe]
Here I would like to mention a principle which I call ‘cosmic loneliness.’ It is relevant to the notion of ‘cosmic silence’ (the fact that we have never received radio signals from an alien civilization). Even if the universe is teaming with life, the scales are so enormous that communication as we know it is highly improbable. Radio signals do not travel further than a few light years, and any kind of information encoded in those signals cannot travel faster than light. Therefore all messages travelling in the universe right now will be rendered obsolete and meaningless after a while. As a consequence it seems that even if information in general or life in particular are common and plentiful in the universe, communication in the form of dialectic conversation was not the original purpose of the universe. This might also make us think if we earthlings communicate with each other because we really enjoy it, or simply because we find it necessary.
An intriguing and also surprising aspect is that the Milky Way, our own galaxy, has an age approximately equal to the age of the universe itself. The thin disk of the Milky Way however is somewhat younger, it was created 5 billion years after the Big Bang:
Night sky from a hypothetical planet within the Milky Way 10 billion years ago
The Milky Way began as one or several small over-densities in the mass distribution in the Universe shortly after the Big Bang. Some of these over-densities were the seeds of globular clusters in which the oldest remaining stars in what is now the Milky Way formed. These stars and clusters now comprise the stellar halo of the Milky Way. Within a few billion years of the birth of the first stars, the mass of the Milky Way was large enough so that it was spinning relatively quickly. Due to conservation of angular momentum, this led the gaseous interstellar medium to collapse from a roughly spheroidal shape to a disk. Therefore, later generations of stars formed in this spiral disk. Most of younger stars, including the Sun, are observed to be in the disk.
Since the first stars began to form, the Milky Way has grown through both galaxy mergers (particularly early in the Milky Way’s growth) and accretion of gas directly from the Galactic halo. The Milky Way is currently accreting material from two of its nearest satellite galaxies, the Large and Small Magellanic Clouds, through the Magellanic Stream. Properties of the Milky Way suggest it has undergone no mergers with large galaxies in the last 10 billion years; its neighbor the Andromeda Galaxy appears to have a more typical history shaped by more recent mergers with relatively large galaxies.
According to recent studies, the Milky Way as well as Andromeda lie in what in the galaxy color- magnitude diagram is known as the green valley, a region populated by galaxies in transition from the blue cloud (galaxies actively forming new stars) to the red sequence (galaxies that lack star formation). Star-formation activity in green valley galaxies is slowing as they run out of star-forming gas in the interstellar medium. In simulated galaxies with similar properties, star formation will typically have been extinguished within about five billion years from now, even accounting for the expected short-term increase in the rate of star formation due to the collision between both the Milky Way and the Andromeda Galaxy.
Several individual stars have been found in the Milky Way’s halo with measured ages very close to the 13.80-billion-year age of the Universe. Measurements of thin disk stars yield an estimate that the thin disk formed 8.8 ± 1.7 billion years ago. These measurements suggest there was a hiatus of almost 5 billion years between the formation of the galactic halo and the thin disk.
[https://en.wikipedia.org/wiki/Milky_Way#Formation]
It seems that conditions were not ripe for life to appear in the early universe. Still, besides the consequences with respect to the true structure of the universe, the age of the Milky Way makes it possible that some, even few, civilizations have had the time to evolve long before we did. For example, if at the moment the thin disk of the Milky Way formed some G-type stars like our Sun also formed, and it took 5 billion years for the first civilizations to appear on those star systems, as long as it took us to evolve in our solar system, then these civilizations will be 5 billion years more advanced than us, if they still exist.
It is intriguing that there are stars whose age is as old as the Big Bang, and that stars in the galactic halo may be slightly older. This may also suggest a different model for the formation of the universe (for example, in the same way galaxies form, by accretion). Besides this, old stars, although having lacked the necessary metallicity in order to have planetary systems, some of them may have harbored life very early in the history the universe. This is the oldest star currently known:
This is a Digitized Sky Survey image of the oldest star with a well-determined age in our galaxy. The aging star, cataloged as HD 140283, lies 190.1 light-years away.
A team of astronomers using NASA’s Hubble Space Telescope has taken an important step closer to finding the birth certificate of a star that’s been around for a very long time. The star could be as old as 14.5 billion years (plus or minus 0.8 billion years), which at first glance would make it older than the universe’s calculated age of about 13.8 billion years, an obvious dilemma.
This ‘Methuselah star,’ cataloged as HD 140283, has been known about for more than a century because of its fast motion across the sky. The high rate of motion is evidence that the star is simply a visitor to our stellar neighborhood. Its orbit carries it down through the plane of our galaxy from the ancient halo of stars that encircle the Milky Way, and will eventually slingshot back to the galactic halo.
This conclusion was bolstered by the 1950s astronomers who were able to measure a deficiency of heavier elements in the star as compared to other stars in our galactic neighborhood. The halo stars are among the first inhabitants of our galaxy and collectively represent an older population from the stars, like our sun, that formed later in the disk. This means that the star formed at a very early time before the universe was largely ‘polluted’ with heavier elements forged inside stars through nucleosynthesis. (The Methuselah star has an anemic 1/250th as much of the heavy element content of our sun and other stars in our solar neighborhood.)
This Methuselah star has seen many changes over its long life. It was likely born in a primeval dwarf galaxy. The dwarf galaxy eventually was gravitationally shredded and sucked in by the emerging Milky Way over 12 billion years ago. The star retains its elongated orbit from that cannibalism event. Therefore, it’s just passing through the solar neighborhood at a rocket-like speed of 800,000 miles per hour. It takes just 1,500 years to traverse a piece of sky with the angular width of the full Moon.
The star, which is at the very first stages of expanding into a red giant, can be seen with binoculars as a 7th-magnitude object in the constellation Libra. Hubble’s observational prowess was used to refine the distance to the star, which comes out to be 190.1 light-years. Once the true distance is known, an exact value for the star’s intrinsic brightness can be calculated. Knowing a star’s intrinsic brightness is a fundamental prerequisite to estimating its age. The new Hubble age estimates reduce the range of measurement uncertainty, so that the star’s age overlaps with the universe’s age.
[https://www.nasa.gov/mission_pages/hubble/science/hd140283.html]
Although the specific star originally formed in the halo of the Milky Way, therefore it might never have been suitable for life as we know it, there are other stars which have always been in our solar neighborhood, and which seem to be as old as the thin disk of the Milky Way (10 billion years old). We will mention such stars, as having been potentially habitable, later on.
As if the enormous distances which separate the stars were not enough, such distances grow bigger with time due to the expansion of the universe. On the small scale the cosmic expansion is not noticeable, but on the large scale it becomes significant. A measure of this cosmic expansion is Hubble’s constant:
This sequence of images taken with NASA’s Hubble Space Telescope chronicles the rhythmic changes in a rare class of variable star (located in the center of each image) in the spiral galaxy M100. This class of pulsating star is called a Cepheid Variable. The Cepheid in this Hubble picture doubles in brightness (24.5 to 25.3 apparent magnitude) over a period of 51.3 days.
[http://hubblesite.org/image/225/news_release/1994-49]
In the 1920s, Edwin Hubble, using the newly constructed 100" telescope at Mount Wilson Observatory, detected variable stars in several nebulae. Nebulae are diffuse objects whose nature was a topic of heated debate in the astronomical community: were they interstellar clouds in our own Milky Way galaxy, or whole galaxies outside our galaxy? This was a difficult question to answer because it is notoriously difficult to measure the distance to most astronomical bodies since there is no point of reference for comparison. Hubble’s discovery was revolutionary because these variable stars had a characteristic pattern resembling a class of stars called Cepheid variables. By knowing the luminosity of a source it is possible to measure the distance to that source by measuring how bright it appears to us: the dimmer it appears the farther away it is. Thus, by measuring the period of these stars (and hence their luminosity) and their apparent brightness, Hubble was able to show that these nebula were not clouds within our own Galaxy, but were external galaxies far beyond the edge of our own Galaxy.
Hubble’s second revolutionary discovery was based on comparing his measurements of the Cepheid-based galaxy distance determinations with measurements of the relative velocities of these galaxies. He showed that more distant galaxies were moving away from us more rapidly:
where v is the speed at which a galaxy moves away from us, and d is its distance. The constant of proportionality Ho is now called the Hubble constant. The common unit of velocity used to measure the speed of a galaxy is km/sec, while the most common unit of for measuring the distance to nearby galaxies is called the Megaparsec (Mpc) which is equal to 3.26 million light years. Thus the units of the Hubble constant are (km/sec)/Mpc.
This discovery marked the beginning of the modern age of cosmology. Today, Cepheid variables remain one of the best methods for measuring distances to galaxies and are vital to determining the expansion rate (the Hubble constant) and age of the universe.
The expansion or contraction of the universe depends on its content and past history. With enough matter, the expansion will slow or even become a contraction. On the other hand, dark energy drives the universe towards increasing rates of expansion. The current best estimate of expansion (the Hubble Constant) is 73.8 km/sec/Mpc.
[https://map.gsfc.nasa.gov/universe/uni_expansion.html]
The aspect of universal expansion is rather ambiguous. Presumably, at the horizon of the observable universe, 13.8 billion light years away, the galaxies will be receding from us with the speed of light, while beyond the observable horizon astronomical objects can be moving away from us at a speed even faster than light. This paradox is commonly resolved by the metric expansion of spacetime (that spacetime can expand faster than light, while photons do not travel faster than light). Still there is a paradox (a point in spacetime beyond the horizon of the observable universe can be receding faster than light). It has been observed that the universe accelerated its expansion about 5 billion years ago:
According to measurements, the universe’s expansion rate was decelerating until about 5 billion years ago due to the gravitational attraction of the matter content of the universe, after which time the expansion began accelerating. The source of this acceleration is currently unknown. Physicists have postulated the existence of dark energy, appearing as a cosmological constant in the simplest gravitational models as a way to explain the acceleration.
[https://en.wikipedia.org/wiki/Metric_expansion_of_space]
This observation coincides with another one which shows that star formation in the universe dropped dramatically during the same period. If this is true then in the near cosmic future the universe will become a vast desert of red dwarfs (stars much smaller than the Sun, so that they live much longer), since more massive stars like our Sun will have died out. An encouraging thought though is that there may be other universes to compensate for the loss of our own universe. Perhaps a better cosmological view will be necessary to accommodate the existence of other universes. If all spacetime was created by the ‘Big Bang,’ then this ‘Big Bang’ will account for all spacetime. But if, for example, we consider an accretion model for the universe (so that the whole universe is a local concentration of matter within a much wider region of spacetime), then the existence of other universes with various sizes and ages will be possible.
Our own Milky Way galaxy is an island within the vast ocean of interstellar dust. While the Milky Way is 100 thousand light years across, the Andromeda galaxy, which is the closest, is located 2.5 million light years away. This is where within the vast spiral structure of our galaxy the Sun and the Earth reside:
Artist’s concept of what astronomers now believe is the overall structure of the spiral arms in our Milky Way galaxy.
We live in an island of stars called the Milky Way, and many know that our Milky Way is a spiral galaxy. In fact, it’s a barred spiral galaxy, which means that our galaxy probably has just two major spiral arms, plus a central bar that astronomers are only now beginning to understand.
Our galaxy is about 100,000 light-years wide. We’re about 25,000 light-years from the center of the galaxy. It turns out we’re not located in one of the Milky Way’s two primary spiral arms. Instead, we’re located in a minor arm of the galaxy. Our local spiral arm is the Orion Arm. It’s between the Sagittarius and Perseus Arms of the Milky Way. It’s approximately 10,000 light years in length. Our sun, the Earth, and all the other planets in our solar system reside within this Orion Arm. We’re located close to the inner rim of this spiral arm, about halfway along its length.
The Orion Arm, or Orion Spur, has other names as well. It’s sometimes simply called the Local Arm, or the Orion-Cygnus Arm, or the Local Spur. It is named for the constellation Orion the Hunter, which is one of the most prominent constellations of the Northern Hemisphere in winter (Southern Hemisphere summer). Some of the brightest stars and most famous celestial objects of this constellation are neighbors of sorts to our sun, located within the Orion Arm. That’s why we see so many bright objects within the constellation Orion – because when we look at it, we’re looking into our own local spiral arm.
[http://earthsky.org/space/does-our-sun-reside-in-a-spiral-arm-of-the-milky-way-galaxy]
Some astronomers have suggested that there is a GHZ (galactic habitable zone) in the Milky way, in the same sense that there is a CHZ (circumstellar habitable zone) in our solar system. Thus as the Earth is located in the middle of the CHZ, in analogy the Sun will be located in the middle of the GHZ. Estimations about the width of such a zone vary. The main argument here is that if not all parts of the Milky Way are suitable for life as we know it, then we may concentrate the search for extraterrestrial life on the habitable areas:
In astrobiology and planetary astrophysics, the galactic habitable zone is the region of a galaxy in which life might most likely develop. More specifically, the concept of a galactic habitable zone incorporates various factors, such as metallicity and the rate of major catastrophes such as supernovae, to calculate which regions of the galaxy are more likely to form terrestrial planets, initially develop simple life, and provide a suitable environment for this life to evolve and advance.
In a paper published in 2001 by astrophysicists Gonzalez, Brownlee and Ward, it is stated that regions near the galactic halo would lack the heavier elements required to produce habitable terrestrial planets, thus creating an outward limit to the size of the galactic habitable zone. Being too close to the galactic center, however, would expose an otherwise habitable planet to numerous supernovae and other energetic cosmic events. Therefore, the authors established an inner boundary for the galactic habitable zone, located just outside the galactic bulge.
Currently the galactic habitable zone is often viewed as an annulus 4-10 kpc (≈13,000-33,000ly) from the galactic center. Galactic habitable zone theory has been criticized due to an inability to quantify accurately the factors making a region of a galaxy favorable for the emergence of life.
[https://en.wikipedia.org/wiki/Galactic_habitable_zone]
Whether the universe is expanding, contacting, or even static, may fundamentally depend on the way we perceive the things around us, either with telescopes or with our own eyes. When we think about the world and the universe, inside our minds no true motion takes place, except from the electric discharges which propagate on our neural network:
Computer simulated image of an area of space more than 50 million light years across, presenting a possible large-scale distribution of light sources in the universe.
[https://en.wikipedia.org/wiki/Observable_universe]
The existence of the universe as a whole and coherent entity is related to the cosmological principle, the aspect that the universe is homogeneous on the large scale. Some cosmologists have argued that homogeneity brakes down at very large scales. Such an argument is supported by the recent discoveries of immense structures at the edge of the observable universe, such as the Huge- Large Quasar Group, or the Hercules- Corona Borealis Great Wall. However the way matter is distributed in the universe is not so significant, as long as the different and distant parts stay together. How the two opposite parts of the universe are instantaneously connected to each other, so that the universe does not collapse, is a great mystery of modern science, because as we believe nothing can travel faster than light. But there seems to be out there a secret network of actions determined by currently unknown laws of physics, waiting to be discovered.
Perhaps this sort of ‘unconscious interconnectedness,’ binding the galaxies in the universe together, and making us able to perceive the word by forming the structure of our own nerve cells, is also responsible for hiding at the same time the deepest nature of the cosmic structure which produced the stars and our thoughts in the first place. Such a fine-tuning between ourselves and the universe also refers to the anthropic principle. But the anthropic principle poses a serious question. In our search for extraterrestrial intelligent lifeforms, which life qualifies as ‘intelligent?’ Which forms qualify as ‘living?’ Should they be just like us? If they use different ways of communication how can we detect them? If their structure consists of exotic matter, how can we perceive them? What exactly are we looking for with our telescopes, beyond perhaps the reflections of our own image?
[http://astronaut.com/whos-revisiting-drake-equation/]
These are some historical aspects about Drake’s equation, according to Wikipedia:
In September 1959, physicists Giuseppe Cocconi and Philip Morrison published an article in the journal Nature with the provocative title ‘Searching for Interstellar Communications.’ Cocconi and Morrison argued that radio telescopes had become sensitive enough to pick up transmissions that might be broadcast into space by civilizations orbiting other stars.
Such messages, they suggested, might be transmitted at a wavelength of 21 cm (1,420.4 MHz). This is the wavelength of radio emission by neutral hydrogen, the most common element in the universe, and they reasoned that other intelligences might see this as a logical landmark in the radio spectrum.
Two months later, Harvard University astronomy professor Harlow Shapley speculated on the number of inhabited planets in the universe, saying “The universe has 10 million, million, million suns similar to our own. One in a million has planets around it. Only one in a million, million, has the right combination of chemicals, temperature, water, days and nights to support planetary life as we know it. This calculation arrives at the estimated figure of 100 million worlds where life has been forged by evolution.”
Seven months after Cocconi and Morrison published their article, Drake made the first systematic search for signals from extraterrestrial intelligent beings. Using the 25 m dish of the National Radio Astronomy Observatory in Green Bank, West Virginia, Drake monitored two nearby Sun-like stars: Epsilon Eridani and Tau Ceti. In this project, which he called Project Ozma, he slowly scanned frequencies close to the 21 cm wavelength for six hours per day from April to July 1960. The project was well designed, inexpensive, and simple by today’s standards. It was also unsuccessful.
Soon thereafter, Drake hosted a ‘search for extraterrestrial intelligence’ meeting on detecting their radio signals. The meeting was held at the Green Bank facility in 1961. The ten attendees were conference organizer J. Peter Pearman, Frank Drake, Philip Morrison, businessman and radio amateur Dana Atchley, chemist Melvin Calvin, astronomer Su-Shu Huang, neuroscientist John C. Lilly, inventor Barney Oliver, astronomer Carl Sagan and radio-astronomer Otto Struve. The equation that bears Drake’s name arose out of his preparations for the meeting.
where
N = the number of civilizations in our galaxy with which communication might be possible.
R∗ = the average rate of star formation in our galaxy
fp = the fraction of those stars that have planets
ne = the average number of planets that can potentially support life per star that has planets
fl = the fraction of planets that could support life that actually develop life at some point
fi = the fraction of planets with life that actually go on to develop intelligent life (civilizations)
fc = the fraction of civilizations that develop a technology that releases detectable signs of their existence into space.
L = the length of time for which such civilizations release detectable signals into space.
The Drake equation amounts to a summary of the factors affecting the likelihood that we might detect radio-communication from intelligent extraterrestrial life. The last four parameters, fl, fi, fc, and L, are not known and are very difficult to estimate, with values ranging over many orders of magnitude. Therefore, the usefulness of the Drake equation is not in the solving, but rather in the contemplation of all the various concepts which scientists must incorporate when considering the question of life elsewhere, and gives the question of life elsewhere a basis for scientific analysis.
There is considerable disagreement on the values of these parameters, but the ‘educated guesses’ used by Drake and his colleagues in 1961 were:
R* = 1 star/y (1 star formed per year, on the average over the life of the galaxy).
fp = 0.2 to 0.5 (one fifth to one half of all stars formed will have planets).
ne = 1 to 5 (stars with planets will have between 1 and 5 planets capable of developing life).
fl = 1 (100% of these planets will develop life).
fi = 1 (100% of which will develop intelligent life).
fc = 0.1 to 0.2 (10–20% of which will be able to communicate).
L = 1,000 to 100,000,000 years (which will last somewhere between 1,000 and 100,000,000 years).
Inserting the above minimum numbers into the equation gives a minimum N of 20. Inserting the maximum numbers gives a maximum N of 50,000,000. Drake states that given the uncertainties, the original meeting concluded that N≈L, and there were probably between 1,000 and 100,000,000 civilizations in the Milky Way galaxy.
The astronomer Carl Sagan speculated that all of the terms, except for the lifetime of a civilization, are relatively high and the determining factor in whether there are large or small numbers of civilizations in the universe is the civilization lifetime, or in other words, the ability of technological civilizations to avoid self-destruction. In Sagan’s case, the Drake equation was a strong motivating factor for his interest in environmental issues and his efforts to warn against the dangers of nuclear warfare.
[https://en.wikipedia.org/wiki/Drake_equation]
There have been various estimates using Drake’s equation. Apart from any criticism, the equation may provide a good exercise for one who would like to delve deeper into the mysteries of the universe, and at the same time understand oneself better. One may even set all frequencies equal to 1, so that the determining factor will be L, the expected lifespan of a communicating intelligent civilization, given that they do want to communicate. This is why Carl Sagan pointed out the role of self-preservation, and environmental protection.
At the moment we know that we have been using detectable communications approximately for the last 100 years:
The first radio news program was broadcast August 31, 1920 by station 8MK in Detroit, Michigan, which survives today as all-news format station WWJ under ownership of the CBS network.
[https://en.wikipedia.org/wiki/History_of_radio]
Thus, in our case, L=100. Setting all other frequencies in Drake’s equation equal to 1, and assuming that the current production rate of new stars in the Milky Way is also approximately equal to 1, then the possible number of other civilizations like our own in the Milky Way will be N=100. If the Neolithic Revolution lasted about 10,000 years on our planet, then L=10,000, and there will be N=10,000 civilizations at the stage of the Neolithic Revolution right now in the Milky Way. If the Stone Age lasted 2.5 million years (since the first evidence of stone-tool use) on our planet, then L=2,500,000, and there will be an equal number N of ‘stone people’ on other planets in the Milky Way. And so on. This will be true if we set the frequencies equal to 1, so that we identify N with L.
In what follows each of the frequencies in Drake’s equation will be explored independently.
The number N* of stars in the Milky Way can be determined if we know the rate R* of new stars, and multiply the rate R* by the lifespan L* of a star, so that it will be
2.2.1 Rate of stars
It is estimated that the Milky Way churns out seven new stars per year:
By mapping patches of radioactive aluminum in the Milky Way, scientists could determine the number of stars that are born and die each year in our galaxy.
In an investigation smacking of forensic detective work, scientists have measured the rate of star death and rebirth in our galaxy by combing through the sparse remains of exploded stars from the last few million years.
The scientists used the European Space Agency’s INTEGRAL (International Gamma-Ray Astrophysics Laboratory) satellite to explore regions of the galaxy shining brightly from the radioactive decay of aluminum-26, an isotope of aluminum. This aluminum is produced in massive star and in their explosions, called supernovae, and it emits a telltale light signal in the gamma-ray energy range. A global spatial distribution model was used to convert the observed gamma-ray flux to a total amount of aluminum-26.
The team’s multi-year analysis revealed three key findings: The team confirmed that aluminum-26 is found primarily in star-forming regions throughout the galaxy; about once every 50 years a massive star will go supernova in our galaxy (yes, we are overdue); and each year our galaxy creates on average about seven new stars. These rates also imply that per year about three to four solar masses of interstellar gas are converted to stars. About ten billion years into its life, the Milky Way galaxy has now converted about 90 percent of its initial gas content into stars.
[http://www.nasa.gov/centers/goddard/news/topstory/2006/milkyway_seven.html]
But if there are about 7 stars born in the Milky each year, which comes about to 3-4 solar masses (so that a star in the Milky Way has an average mass of about 0.5 times the mass of our Sun), how many stars die at the same time? Roughly speaking, we may have one star dying in the Milky Way, for each new star which is born:
We usually talk of star formation in terms of the gas mass that is converted into stars each year. We call this the star formation rate. In the Milky Way right now, the star formation rate is about 3 solar masses per year (i.e. three times the mass of the Sun’s worth of star is produced each year). The stars formed can either be more or less massive than the Sun, though less massive stars are more numerous. So roughly if we assume that on average the stars formed have the same mass as the Sun, then the Milky Way produces about 3 new stars per year. People often approximate this by saying there is about 1 new star per year.
Now what about the rate at which stars die? In typical galaxies like the Milky Way, a massive star should end its life as a supernova about every 100 years. Less massive stars (like the Sun) end their lives as planetary nebulae, leading to the formation of white dwarfs. There are about one of these per year.
Therefore we get on average about one new star per year, and one star dying each year as a planetary nebula in the Milky Way. These rates are different in different types of galaxies, but you can say that this is roughly the average over all galaxies in the Universe. We estimate at about 100 billion the number of galaxies in the observable Universe, therefore there are about 100 billion stars being born and dying each year, which corresponds to about 275 million per day, in the whole observable Universe.
[http://curious.astro.cornell.edu/about-us/83-the-universe/stars-and-star-clusters/star-formation-and-molecular-clouds/400-how-many-stars-are-born-and-die-each-day-beginner]
The approximation of 1 star dying- 1 star born, roughly means that our Milky Way galaxy is reaching a stage of equilibrium, where currently the rate of new stars is approximately equal to zero, so that we are close to the peak population of stars. This may be fundamental for the appearance of life in star systems, because an equilibrium may create stable conditions for the appearance and maintenance of life.
2.2.2 Lifespan of stars
Our Sun is not an average star in the Milky Way, as its mass is considerably larger (twice as much or even bigger) than the average star’s. The average star in the Milky Way is in fact a low- mass red dwarf. Red dwarfs are much more numerous and they live much longer than our Sun. The less massive a star is, the longer it lives. However whether red dwarfs can sustain life is debatable.
The lifespan of a star is estimated as follows:
Representative lifetimes of stars as a function of their masses
Stellar evolution is the process by which a star changes over the course of time. Depending on the mass of the star, its lifetime can range from a few million years for the most massive to trillions of years for the least massive, which is considerably longer than the age of the universe. The table shows the lifetimes of stars as a function of their masses. All stars are born from collapsing clouds of gas and dust, often called nebulae or molecular clouds. Over the course of millions of years, these protostars settle down into a state of equilibrium, becoming what is known as a main-sequence star.
Nuclear fusion powers a star for most of its life. Initially the energy is generated by the fusion of hydrogen atoms at the core of the main-sequence star. Later, as the preponderance of atoms at the core becomes helium, stars like the Sun begin to fuse hydrogen along a spherical shell surrounding the core. This process causes the star to gradually grow in size, passing through the subgiant stage until it reaches the red giant phase. Stars with at least half the mass of the Sun can also begin to generate energy through the fusion of helium at their core, whereas more-massive stars can fuse heavier elements along a series of concentric shells. Once a star like the Sun has exhausted its nuclear fuel, its core collapses into a dense white dwarf and the outer layers are expelled as a planetary nebula. Stars with around ten or more times the mass of the Sun can explode in a supernova as their inert iron cores collapse into an extremely dense neutron star or black hole. Although the universe is not old enough for any of the smallest red dwarfs to have reached the end of their lives, stellar models suggest they will slowly become brighter and hotter before running out of hydrogen fuel and becoming low-mass white dwarfs.
[https://en.wikipedia.org/wiki/Stellar_evolution]
On average, main-sequence stars are known to follow an empirical mass-luminosity relationship. The luminosity (L) of the star is roughly proportional to the total mass (M) as the following power law:
The amount of fuel available for nuclear fusion is proportional to the mass of the star. Thus, the lifetime of a star on the main sequence can be estimated by comparing it to solar evolutionary models. The Sun has been a main-sequence star for about 4.5 billion years and it will become a red giant in 6.5 billion years, for a total main sequence lifetime of roughly 1010 years. Hence:
where M and L are the mass and luminosity of the star, respectively, M☉ is a solar mass, L☉ is the solar luminosity and τMS is the star’s estimated main sequence lifetime.
Although more massive stars have more fuel to burn and might intuitively be expected to last longer, they also radiate a proportionately greater amount with increased mass. This is required by the stellar equation of state; for a massive star to maintain equilibrium, the outward pressure of radiated energy generated in the core not only must but will rise to match the titanic inward gravitational pressure of its envelope. Thus, the most massive stars may remain on the main sequence for only a few million years, while stars with less than a tenth of a solar mass may last for over a trillion years.
[https://en.wikipedia.org/wiki/Main_sequence]
Thus this is a way to estimate the rate of new stars in the Milky Way. Assuming an average mass MAV for MS (main sequence) stars of 0.4M☉ (solar masses), the timespan τMS of an average MS star will be,
Therefore if N* is the total number of MS stars in the Milky Way, and we identify the lifespan L* of an average MS star with the time τMS, then the rate R* of new MS stars will be,
2.2.3 Habitability of red dwarf systems
Although red dwarfs are the most abundant and long-lived MS stars in the Milky Way, many of which are observed to have terrestrial planets in orbit, so that such planetary systems would be the most common, the habitability of planets orbiting red dwarfs is debated:
Proxima Centauri, the closest star to the Sun at 4.2ly, is a red dwarf
A red dwarf is a small and relatively cool star on the main sequence, either K or M spectral type. Red dwarfs range in mass from a low of 0.075 solar masses to about 0.50 and have a surface temperature of less than 4,000 K (5,778 K has the sun).
Red dwarfs are by far the most common type of star in the Milky Way, at least in the neighborhood of the Sun, but because of their low luminosity, individual red dwarfs cannot easily be observed. From Earth, not one is visible to the naked eye. Proxima Centauri, the nearest star to the Sun, is a red dwarf, as are twenty of the next thirty nearest stars. According to some estimates, red dwarfs make up three-quarters of the stars in the Milky Way.
Stellar models indicate that red dwarfs less than 0.35 solar masses are fully convective. Hence the helium produced by the thermonuclear fusion of hydrogen is constantly remixed throughout the star, avoiding a buildup at the core. Red dwarfs therefore develop very slowly, having a constant luminosity and spectral type for, in theory, some trillions of years, until their fuel is depleted. Because of the comparatively short age of the universe, no red dwarfs of advanced evolutionary stages exist.
All observed red dwarfs contain metals, which in astronomy are elements heavier than hydrogen and helium. The Big Bang model predicts that the first generation of stars should have only hydrogen, helium, and trace amounts of lithium. With their extreme lifespans, any red dwarfs that were part of that first generation should still exist today. There are several explanations for the missing population of metal-poor red dwarfs. The preferred explanation is that, without heavy elements, only large stars can form. Large stars rapidly burn out and explode as supernova, spewing heavy elements that then allow red dwarfs to form. Alternative explanations, such as metal-poor red dwarfs being dim and few in number, are considered less likely because they seemingly conflict with stellar evolution models.
Many red dwarfs are orbited by exoplanets but large Jupiter-sized planets are comparatively rare. Doppler surveys around a wide variety of stars indicate about 1 in 6 stars having twice the mass of the Sun are orbited by one or more Jupiter-sized planets, vs. 1 in 16 for Sun-like stars and only 1 in 50 for red dwarfs. On the other hand, microlensing surveys indicate that long-period Neptune-mass planets are found around 1 in 3 red dwarfs. Observations with HARPS further indicate 40% of red dwarfs have a ‘super-Earth’ class planet orbiting in the habitable zone where liquid water can exist on the surface of the planet.
Planetary habitability of red dwarf systems is subject to some debate. In spite of their great numbers and long lifespans, there are several factors which may make life difficult on planets around a red dwarf. First, planets in the habitable zone of a red dwarf would be so close to the parent star that they would likely be tidally locked. This would mean that one side would be in perpetual daylight and the other in eternal night. This could create enormous temperature variations from one side of the planet to the other. Such conditions would appear to make it difficult for forms of life similar to those on Earth to evolve. And it appears there is a great problem with the atmosphere of such tidally locked planets: the perpetual night zone would be cold enough to freeze the main gases of their atmospheres, leaving the daylight zone nude and dry. On the other hand, recent theories propose that either a thick atmosphere or planetary ocean could potentially circulate heat around such a planet.
Variability in stellar energy output may also have negative impacts on the development of life. Red dwarfs are often flare stars, which can emit gigantic flares, doubling their brightness in minutes. This variability may also make it difficult for life to develop and persist near a red dwarf. It may be possible for a planet orbiting close to a red dwarf to keep its atmosphere even if the star flares. However, more-recent research suggests that these stars may be the source of constant high-energy flares and very large magnetic fields, diminishing the possibility of life as we know it. Whether this is a peculiarity of the star under examination or a feature of the entire class remains to be determined.
[https://en.wikipedia.org/wiki/Red_dwarf]
Perhaps life could exist on a planet orbiting a red dwarf under special conditions. For example, such lifeforms may live underground most of the time. But adaptations which we commonly attribute to intelligence (e.g. living on the surface of a planet may be necessary for the evolution of bipedalism) may not be available. Furthermore, despite the intense flare activity of red dwarfs, their energy output is much lower than that of a Sun-like star, so that even if some of those lifeforms have evolved enough to have become complex, the energy shortage may prevent them from advancing further on. Thus a form of evolutionary ‘dwarfism,’ synonymous to the nature of a red-dwarf star, could be expected forever.
2.2.4 Populations of stars
Relatively recent observations show that the first stars appeared in the universe very early:
Results from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) released in February 2003 show that the first stars formed when the universe was only about 200 million years old. Observations by WMAP also revealed that the universe is currently about 13.7 billion years old. So it was very early in the time after the Big Bang explosion that stars formed.
Observations reveal that tiny clumps of matter formed in the baby universe; to WMAP, these clumps are seen as tiny temperatures differences of less than one-millionth of a degree. Gravity then pulled in more matter from areas of lower density and the clumps grew. After about 200 million years of this clumping, there was enough matter in one place that the temperature got high enough for nuclear fusion to begin - providing the engine for stars to glow.
[http://starchild.gsfc.nasa.gov/docs/StarChild/questions/question55.html]
However, this first stars were very short-lived:
The incredibly bright and old CR7 galaxy, captured here in an artist’s impression, seems to shelter some of the universe’s earliest stars. This is the first time this type of star has ever been identified.
The first stars to condense after the Big Bang, called Population III stars, would have been up to a 1,000 times larger than the sun. These Population III stars would have been short-lived, exploding as supernovas after just 2 million years of blazing life, releasing the elements they created. Later stars could form from those remnants and forge even heavier elements.
[http://www.space.com/29685-bright-galaxy-first-stars-universe.html]
Stars can be divided into three groups, according to the population which they belong to:
Population I (or Generation III), or metal-rich stars, are young stars with the highest metallicity out of all three populations. The Earth’s Sun is an example of a metal-rich star. These are common in the spiral arms of the Milky Way galaxy.
Generally, the youngest stars, the extreme population I, are found farther toward the center of a galaxy, and intermediate population I stars are farther out. The Sun is an intermediate population I star. Population I stars have regular elliptical orbits of the galactic center, with a low relative velocity.
Between the intermediate population I and the population II stars comes the intermediary disc population.
Population II (or Generation II), or metal-poor stars, are those with relatively little metal. Intermediate population II stars are common in the bulge near the center of our galaxy, whereas population II stars found in the galactic halo are older and thus more metal-poor. Globular clusters also contain high numbers of population II stars.
Population III (or Generation I), or extremely metal-poor stars (EMP), are a hypothetical population of extremely massive and hot stars with virtually no metals, except possibly for intermixing ejecta from other nearby Pop III supernovae. Their existence is inferred from cosmology, but they have not yet been observed directly.
It was hypothesized that the high metallicity of population I stars makes them more likely to possess planetary systems than the other two populations, because planets, particularly terrestrial planets, are thought to be formed by the accretion of metals. However, observations of the Kepler data-set have found smaller planets around stars with a range of metallicities, while only larger, potential gas giant planets are concentrated around stars with relatively higher metallicity- a finding that has implications for theories of gas giant formation.
[https://en.wikipedia.org/wiki/Stellar_population]
Since the earlier a star formed in the universe the poorer in metals it might be, the role of metallicity is important in determining whether a metal-poor star can support a planetary system, and if such a planetary system is suitable for life:
This image shows the critical metallicity for Earth-like planet formation, expressed as iron abundance relative to that of the Sun, as a function of distance (r) from the host star.
In new research, scientists have attempted to determine the precise conditions necessary for planets to form in a star system. Jarrett Johnson and Hui Li of Los Alamos National Laboratory assert that observations increasingly suggest that planet formation takes place in star systems with higher metallicities.
Astronomers use the term ‘metallicity’ in reference to elements heavier than hydrogen and helium, such as oxygen, silicon, and iron. In the ‘core accretion’ model of planetary formation, a rocky core gradually forms when dust grains that make up the disk of material that surrounds a young star bang into each other to create small rocks known as ‘planetesimals.’
Citing this model, Johnson and Li stress that heavier elements are necessary to form the dust grains and planetesimals which build planetary cores. Additionally, evidence suggests that the circumstellar disks of dust that surround young stars don’t survive as long when the stars have lower metallicities. The most likely reason for this shorter lifespan is that the light from the star causes clouds of dust to evaporate. Johnson and Li further state that disks with higher metallicity tend to form a greater number of high mass giant planets.
In order to obtain estimates of the critical metallicity necessary for planet formation, Johnson and Li compared the lifetime of the disk and the length of time required for dust grains in the disk to settle. Since the settling time for dust grains depends on the density and temperature of the disk, which are related to the distance from the host star, the critical metallicity is also a function of distance from the host star.
The team found that the formation of planetesimals can only take place once a minimum metallicity is reached in a proto-stellar disk. Since the earliest stars that formed in the universe (Population III stars) do not have the required metallicity to host planets, it is believed that the supernova explosions from such stars helped enrich subsequent (Population II) stars, some of which may still be in existence and could host planets.
Johnson and Li also note that the formation of Earth-like planets is not itself a sufficient prerequisite for life to take hold, stating that early galaxies contained numerous supernovae and black holes- both strong sources of radiation that would threaten life. Given the hostile conditions in the early universe, it is expected that conditions suitable for life were only present after early galaxy formation.
[http://www.astrobio.net/news-exclusive/when-stellar-metallicity-sparks-planet-formation/]
2.2.5 Peak population of MS stars
The aspect that the vast majority of MS stars are red dwarfs can be interpreted as an indication that the Milky Way has exhausted most of its interstellar gas reserves, so that most of the stars it produces are low mass stars (red dwarfs). This is also supported by the following observation:
Diagram above shows how star production has decreased over billions of years. The new results indicate that, measured by mass, the production rate of stars has dropped by 97 percent since its peak 11 billion years ago.
For years, scientists were confused by the disparity between the number of stars we can observe and the number of stars we know should have been created by the universe. Numerous studies have each looked at specific periods in our Universe’s history in order to assess star formation, however since multiple methods were used, it was fairly difficult to aggregate and establish a comparative conclusion.
A team of international researchers decided to run a complete survey from the very dawn of the first stars using three telescopes- the UK Infrared Telescope and the Subaru Telescope, both in Hawaii, and Chile’s Very Large Telescope. Snapshots were taken of the look of the Universe at various instances in time when it was 2, 4, 6 and 9 billion years old- that’s 10 times as large as any previous similar study. The astronomers concluded that the rate of formation of new stars in the Universe is now only 1/30th of its peak.
“You might say that the universe has been suffering from a long, serious ‘crisis:’ cosmic GDP output is now only 3 percent of what it used to be at the peak in star production!” said David Sobral of the University of Leiden in the Netherlands.
“If the measured decline continues, then no more than 5 percent more stars will form over the remaining history of the cosmos, even if we wait forever. The research suggests that we live in a universe dominated by old stars.”
According to the current accepted models of the Universe’s evolution, stars first began to form some 13.4 billion years ago, or 300 million years after the Big Bang. Now, these ancient stars were nothing like those commonly found throughout the cosmos. These were like titans with respect to Olympus’ gods- standing at hundreds of times more massive than our sun. Alas, the giants’ life would’ve been short lived, quickly exhausting their fuel, they had only one million years or so worth of time. Lighter stars, like our own, in contrast can shine long and bright for billions of years.
It’s from these huge, first stars that other smaller, more long-lived stars form as the cosmic dust was recycled. Our Sun, for example, is thought to be a third generation star, and has a typical mass, or weight, by today’s standards. To identify star formations, the astronomers searched for alpha particles emitted by hydrogen atoms, appearing as a bright red light.
“Half of these were born in the ‘boom’ that took place between 11 and 9 billion years ago and it took more than five times as long to produce the rest,” Sobral said. “The future may seem rather dark, but we’re actually quite lucky to be living in a healthy, star-forming galaxy which is going to be a strong contributor to the new stars that will form.
[http://www.zmescience.com/space/universe-stop-making-news-stars-04343/]
The previous observation may seem discouraging, but in fact the opposite could be true: If the maximum rate of stars occurred approximately 4-5 billion years after the Big Bang, and if the lifespan of a star like our Sun is roughly 10-12 billion years, then the peak population of Sun-like stars (those with a mass about equal to the mass of the Sun) will occur about 15-16 billion years after the Big Bang, or a couple of billion years, give or take, from now. If we also assume a time difference of about 5 billion years for an intelligent civilization to appear in a Sun-like star system (as long as it took us), then the peak population of civilizations in the Milky Way will occur about 20 billion years after the Big Bang, or about 5-6 billion years from now. If this true then the problem of ‘cosmic silence’ (that it seems we are alone in the universe) could find an explanation, since a small fraction of civilizations will have already emerged.
2.2.6 Generations of civilizations
Although relatively early in the history of the universe conditions may not have been ripe for the appearance of life in planetary systems, while planetary systems may have been sparse because of the low metallicity of the parent stars, in some Population II stars life may have had the opportunity to appear and evolve. This is a related article:
“How long has our galaxy harbored Class F, G, and K stars with potentially life-sustaining terrestrial planets? I’ve pondered this question for a while and tried to get answers from the web to no avail.
However, it just occurred to me that our sun, and other main sequence stars of 0.3 to 8 solar masses, will eventually become Red Giants. Therefore, the Red Giants we see today (e.g. Aldebaran, Arcturus, Gamma Cruces, etc.) used to be sun-like and, as such, probably had habitable zones for billions of years. Moreover, Aldebaran appears to me to be a Population I Star, meaning that it has a metallicity comparable to our sun’s; a trait that is associated with the development of terrestrial planets.
Since it would take another 5 billion years for our sun to become a Red Giant, we can extrapolate that Aldebaran et al may have possessed potentially life-bearing planets as early as 5 billion years ago, most likely more.
[https://www.quora.com/How-long-has-our-galaxy-harbored-Class-F-G-and-K-stars-with-potentially-life-sustaining-terrestrial-planets]
This is the oldest planetary system which has ever been found (as of 27 January 2015):
This is an artistic impression of the Kepler-444 planetary system
[http://www.sci-news.com/astronomy/science-kepler-444-five-exoplanets-11-billion-year-old-star-02437.html]
Kepler-444 is a star system which consists of an orange main sequence primary star of spectral type K0, and a pair of M-dwarf stars, 116 light-years away from Earth in the constellation Lyra. The system is approximately 11.2 billion years old, more than 80% of the age of the universe, whereas the Sun is only 4.6 billion years old.
On 27 January 2015, the Kepler spacecraft is reported to have confirmed the detection of five sub-Earth-sized rocky exoplanets orbiting the primary star. Preliminary results of the planetary system around Kepler-444 were first announced at the second Kepler science conference in 2013. The original research on Kepler-444 was published in The Astrophysical Journal on 27 January 2015.
All five rocky exoplanets are smaller than the size of Venus (but bigger than Mercury) and each of the exoplanets completes an orbit around the host star in less than 10 days. Even the furthest planet, Kepler-444f, still orbits closer to the star than Mercury is to the Sun. According to NASA, no life as we know it could exist on these hot exoplanets, due to their close orbital distances to the host star.
[https://en.wikipedia.org/wiki/Kepler-444]
As far as Aldebaran is concerned, it is classified as a type K5 III star, which indicates it is an orange-hued giant star that has evolved off the main sequence. It is also possible that the star is orbited by a hot Jupiter.
[https://en.wikipedia.org/wiki/Aldebaran]
If this is true then this is another example of an old star with a planetary system. If Aldebaran used to be a K-type main sequence star then, since the mass of K- type stars is less than the mass of G-type stars (like our Sun), so that they live longer, its age will be at least 10 billion years. Even if in the case of Aldebaran or Kepler-444 the planets are too close to the parent star, sooner or later old, population II, stars may be discovered with terrestrial planets in the habitable zone. If such stars were born 5 billion years after the Big Bang, as soon as the thin disk of the Milky Way formed, and if it took life another 5 billion years or so to appear and evolve (as long as it took intelligent life to appear on Earth), then it is possible that right now in the Milky Way there are some population II (or generation II) civilizations 5 billion years more advanced than we are, being at the stage of evacuating their dying host star, moving towards other star systems. Thus if we just call those civilizations the 1st generation (corresponding to the 2nd generation of stars, since life in 1st generation star systems would have been impossible as we know it), then we might regard ourselves as belonging to the 2nd generation of civilizations. Presumably a 3rd generation of civilizations will follow, as another generation of stars like our Sun (the last of them) is born in the Milky Way right now.
One might think that there is something special about the Sun as a star and the Earth as a planet, so that, perhaps, planets are rare in other solar systems. However it seems that planets are not the exception but the rule, as the Kepler Space Telescope discovers more and more planets:
Histogram of exoplanets by size- the gold bars represent Kepler’s latest newly verified exoplanets (May 10, 2016).
Kepler space observatory was launched by NASA on March 7, 2009 to discover Earth-size planets orbiting other stars, and estimate how many of the billions of stars in the Milky Way have such planets. Kepler continually monitors over 145,000 main sequence stars in a fixed field of view which contains portions of the constellations Cygnus, Lyra, and Draco.
In November 2013, astronomers estimated, based on Kepler space mission data, that there could be as many as 40 billion rocky, Earth-size exoplanets orbiting in the habitable zones of Sun-like stars and red dwarfs within the Milky Way. It is estimated that 11 billion of these planets may be orbiting Sun-like stars. The nearest such planet may be 3.7 parsecs (12ly) away, according to the scientists.
On February 26, 2014, NASA announced the discovery of 715 newly verified exoplanets around 305 stars by the Kepler Space Telescope. 95% of the discovered exoplanets were smaller than Neptune and four, including Kepler-296f, were less than 2 1/2 the size of Earth and were in habitable zones where surface temperatures are suitable for liquid water.
As of January 2015, Kepler and its follow-up observations had found 1,013 confirmed exoplanets in about 440 star systems, along with a further 3,199 unconfirmed planet candidates.
On May 10, 2016, NASA announced that Kepler mission has verified 1,284 new planets. Based on their size, about 550 could be rocky planets. Nine of these orbit in their stars’ habitable zone.
[https://en.wikipedia.org/wiki/Kepler_(spacecraft)]
[https://en.wikipedia.org/wiki/List_of_exoplanets_discovered_using_the_Kepler_spacecraft]
This is the related press release from NASA:
This artist’s concept depicts select planetary discoveries made to date by NASA’s Kepler space telescope.
NASA’s Kepler mission has verified 1,284 new planets- the single largest finding of planets to date. In the newly-validated batch of planets, nearly 550 could be rocky planets like Earth, based on their size. Nine of these orbit in their sun’s habitable zone, which is the distance from a star where orbiting planets can have surface temperatures that allow liquid water to pool. With the addition of these nine, 21 exoplanets now are known to be members of this exclusive group.
“This announcement more than doubles the number of confirmed planets from Kepler,” said Ellen Stofan, chief scientist at NASA Headquarters in Washington. “This gives us hope that somewhere out there, around a star much like ours, we can eventually discover another Earth.”
Kepler captures the discrete signals of distant planets- decreases in brightness that occur when planets pass in front of, or transit, their stars- much like the May 9 Mercury transit of our sun. Since the discovery of the first planets outside our solar system more than two decades ago, researchers have resorted to a laborious, one-by-one process of verifying suspected planets.
Analysis was performed on the Kepler space telescope’s July 2015 planet candidate catalog, which identified 4,302 potential planets. For 1,284 of the candidates, the probability of being a planet is greater than 99 percent- the minimum required to earn the status of ‘planet.’ An additional 1,327 candidates are more likely than not to be actual planets, but they do not meet the 99 percent threshold and will require additional study. The remaining 707 are more likely to be some other astrophysical phenomena. This analysis also validated 984 candidates previously verified by other techniques.
“Before the Kepler space telescope launched, we did not know whether exoplanets were rare or common in the galaxy. Thanks to Kepler and the research community, we now know there could be more planets than stars,” said Paul Hertz, Astrophysics Division director at NASA Headquarters. “This knowledge informs the future missions that are needed to take us ever-closer to finding out whether we are alone in the universe.”
Of the nearly 5,000 total planet candidates found to date, more than 3,200 now have been verified, and 2,325 of these were discovered by Kepler. Launched in March 2009, Kepler is the first NASA mission to find potentially habitable Earth-size planets. For four years, Kepler monitored 150,000 stars in a single patch of sky, measuring the tiny, telltale dip in the brightness of a star that can be produced by a transiting planet. In 2018, NASA’s Transiting Exoplanet Survey Satellite will use the same method to monitor 200,000 bright nearby stars and search for planets, focusing on Earth and Super-Earth-sized.
[https://www.nasa.gov/press-release/nasas-kepler-mission-announces-largest-collection-of-planets-ever-discovered]
This is the number of exoplanets according to NASA (as of 2/27/2018):
Star Systems
|
Candidates
|
Confirmed planets
|
Terrestrial
|
Super-Earth
|
Neptune-like
|
Gas Giant
|
Unknown
|
2,759
|
4,496
|
3,704
|
929
|
55
|
1,482
|
1,211
|
27
|
100%
|
25.1%
|
1.5%
|
40%
|
32.7%
|
0.7%
|
Out of approximately 4,000 confirmed planets, about 1,000 of them are terrestrial (rocky). This is 25% more or less. For all the 3,000 or so star systems, there are about 1.3 confirmed planets per star system. Probably the number of planets per solar system will increase if our own multi-planetary system is not the exception. However not all of the terrestrial planets will orbit Sun-like stars. Most of them will be orbiting red dwarfs, which constitute the majority of MS stars. If 75% of all MS stars are red dwarfs, then there will be no more than (25%)(25%)=6.25% terrestrial planets orbiting Sun-like stars (MS stars with a mass close to that of our sun). Additionally not all of the remaining terrestrial planets will be found in the star’s habitable zone. If just another 25% of them is in the habitable zone, then (6.25%)(25%)=1.5625% of all planets will be habitable. Furthermore not all of those 1%-2% Earth-like habitable planets may have developed life, and even fewer may be occupied by intelligent life as we know it. Still out of about 1,500 star systems which are found within a radius of 50ly from the Sun, there could be as many as 30 habitable Earth-like planets, or out of approximately 50 star systems which are found within a radius of about 15ly from the Sun, 1 such planet could exist.
2.3.1 Earth analog
Talking about Earth-like planets, how are they defined? A related notion is the ‘Earth analog:’
An Earth analog is a planet or moon with environmental conditions similar to those found on Earth.
The possibility is of particular interest to astrobiologists and astronomers under reasoning that the more similar a planet is to Earth, the more likely it is to be capable of sustaining complex extraterrestrial life. As such, it has long been speculated and the subject expressed in science, philosophy, science fiction and popular culture. Advocates of space colonization have long sought an Earth analog as a ‘second home,’ while advocates for space and survival would regard such a planet as a potential ‘new home’ for humankind.
Before the scientific search for and study of extrasolar planets, the possibility was argued through philosophy and science fiction. The mediocrity principle suggests that planets like Earth should be common in the universe, while the Rare Earth hypothesis suggests that they are extremely rare. The thousands of exoplanetary star systems discovered so far are profoundly different from our solar system, supporting the Rare Earth hypothesis.
Philosophers have pointed out that the size of the universe is such that a near-identical planet must exist somewhere. In the far future, technology may be used by humans to artificially produce an Earth analog by terraforming. The multiverse theory suggests that an Earth analog could exist in another universe or even be another version of the Earth itself in a parallel universe.
The probability of finding an Earth analog depends mostly on the attributes that are expected to be similar, and these vary greatly. Generally it is considered that it would be a terrestrial planet and there have been several scientific studies aimed at finding such planets. Often implied but not limited to are such criteria as planet size, surface gravity, star size and type (i.e. Solar analog), orbital distance and stability, axial tilt and rotation, similar geography, oceans, air and weather conditions, strong magnetosphere and even the presence of Earth-like complex life.
Size is often thought to be a significant factor, as planets of Earth’s size are thought more likely to be terrestrial in nature and be capable of retaining an Earth-like atmosphere. The list includes planets within the range of 0.8-1.9 Earth masses, below which are generally classed as sub-Earth and above classed as super-Earth. In addition, only planets known to fall within the range of 0.5- 2.0 Earth radius (between half and twice the radius of the Earth) are included.
Scientific findings since the 1990s have greatly influenced the scope of the fields of astrobiology, models of planetary habitability and the search for extraterrestrial intelligence (SETI). Scientists estimate that there may be billions of Earth-size planets within the Milky Way galaxy alone. NASA and SETI have proposed categorizing the increasing number of planets found using a measure called the Earth Similarity Index (ESI) based on mass, radius and temperature. According to this measure, as of 23 July 2015, the confirmed planet currently thought to be most similar to Earth on mass, radius and temperature is Kepler-438b.
[https://en.wikipedia.org/wiki/Earth_analog]
However the planet Kepler-438b may not be suitable for life as we know it after all:
In the Earth Similarity Index (ESI), which measures how similar are planets to Earth as to physics and chemistry, with 1.00 being the most similar, Kepler-438b has an index of 0.88, the highest known for a confirmed exoplanet to date, making it currently the most Earth-like planet in terms of radius and stellar flux. However it has been found that this planet is subjected to powerful radiation activity from its parent star every 100 days, much more violent storms than the stellar flares emitted by the Sun and which would be capable of sterilizing life on Earth. The planet is more likely to resemble a larger and cooler version of Venus.
[https://en.wikipedia.org/wiki/Kepler-438b]
2.3.2 Habitable zone
Either a planet is terrestrial (Earth- like) or a Super- Earth (somewhat larger than the Earth), the distance of the planet from the host star is significant for the temperature on the planet and the presence of liquid water on its surface. The circumstellar habitable zone (CHZ) is defined as follows:
A diagram depicting the Habitable Zone (HZ) boundaries, and how the boundaries are affected by star type. This new plot includes solar system planets (Venus, Earth, and Mars) as well as especially significant exoplanets such as TRAPPIST-1d, Kepler 186f, and our nearest neighbor Proxima Centauri B.
In astronomy and astrobiology, the circumstellar habitable zone (CHZ), also called the Goldilocks zone, or simply the habitable zone, is the range of orbits around a star within which a planetary surface can support liquid water given sufficient atmospheric pressure. The bounds of the CHZ are based on Earth’s position in the Solar System and the amount of radiant energy it receives from the Sun. Due to the importance of liquid water to Earth’s biosphere, the nature of the CHZ and the objects within is thought to be instrumental in determining the scope and distribution of Earth-like extraterrestrial life and intelligence.
Estimates for the habitable zone within the Solar System range from 0.5 to 3.0 astronomical units, though arriving at these estimates has been challenging for a variety of reasons. The inner edge of the HZ is the distance where runaway greenhouse effect vaporize the whole water reservoir and, as a second effect, induce the photo-dissociation of water vapor and the loss of hydrogen to space. The outer edge of the HZ is the distance from the star where adding more carbon dioxide to the atmosphere fails to keep the surface of the planet above the freezing point.
Whether a body is in the circumstellar habitable zone of its host star is dependent on the radius of the planet’s orbit (for natural satellites, the host planet’s orbit), the mass of the body itself, and the radiative flux of the host star. Given the large spread in the masses of planets within a circumstellar habitable zone, coupled with the discovery of super-Earth planets which can sustain thicker atmospheres and stronger magnetic fields than Earth, circumstellar habitable zones are now split into two separate regions- a ‘conservative habitable zone’ in which lower-mass planets like Earth or Venus can remain habitable, complemented by a larger ‘extended habitable zone’ in which super-Earth planets, with stronger greenhouse effects, can have the right temperature for liquid water to exist at the surface.
Since the concept was first presented in 1953, many stars have been confirmed to possess a CHZ planet, including some systems that consist of multiple CHZ planets. Most such planets, being super-Earths or gas giants, are more massive than Earth, because such planets are easier to detect. The CHZ is also of particular interest to the emerging field of habitability of natural satellites, because planetary-mass moons in the CHZ might outnumber planets.
[https://en.wikipedia.org/wiki/Circumstellar_habitable_zone]
An interesting question could be the following one: In solar systems with just one planet, is it more probable that the planet is located in the CHZ? Or does a sufficiently large number of planets is necessary so that one of them can be found in the CHZ?
This is an example of an extrasolar multi-planetary system:
This artist’s concept shows what the TRAPPIST-1 planetary system may look like, based on available data about the planets’ diameters, masses and distances from the host star.
NASA’s Spitzer Space Telescope has revealed a new exoplanet discovery: the first known system of seven Earth-size planets around a single star. Three of these planets are firmly located in the habitable zone, the area around the parent star where a rocky planet is most likely to have liquid water.
The discovery sets a new record for greatest number of habitable-zone planets found around a single star outside our solar system. All of these seven planets could have liquid water- key to life as we know it- under the right atmospheric conditions, but the chances are highest with the three in the habitable zone.
At about 40 light-years (235 trillion miles) from Earth, the system of planets is relatively close to us, in the constellation Aquarius. Because they are located outside of our solar system, these planets are scientifically known as exoplanets.
This exoplanet system is called TRAPPIST-1, named for The Transiting Planets and Planetesimals Small Telescope (TRAPPIST) in Chile. In May 2016, researchers using TRAPPIST announced they had discovered three planets in the system. Assisted by several ground-based telescopes, including the European Southern Observatory’s Very Large Telescope, Spitzer confirmed the existence of two of these planets and discovered five additional ones, increasing the number of known planets in the system to seven. Using Spitzer data, the team precisely measured the sizes of the seven planets and developed first estimates of the masses of six of them, allowing their density to be estimated.
Based on their densities, all of the TRAPPIST-1 planets are likely to be rocky. Further observations will not only help determine whether they are rich in water, but also possibly reveal whether any could have liquid water on their surfaces. The mass of the seventh and farthest exoplanet has not yet been estimated- scientists believe it could be an icy, ‘snowball-like’ world, but further observations are needed.
In contrast to our sun, the TRAPPIST-1 star- classified as an ultra-cool dwarf- is so cool that liquid water could survive on planets orbiting very close to it, closer than is possible on planets in our solar system. All seven of the TRAPPIST-1 planetary orbits are closer to their host star than Mercury is to our sun. The planets also are very close to each other. If a person were standing on one of the planet’s surface, they could gaze up and potentially see geological features or clouds of neighboring worlds, which would sometimes appear larger than the moon in Earth’s sky.
The planets may also be tidally locked to their star, which means the same side of the planet is always facing the star, therefore each side is either perpetual day or night. This could mean they have weather patterns totally unlike those on Earth, such as strong winds blowing from the day side to the night side, and extreme temperature changes.
Following up on the Spitzer discovery, NASA’s Hubble Space Telescope has initiated the screening of four of the planets, including the three inside the habitable zone. These observations aim at assessing the presence of puffy, hydrogen-dominated atmospheres, typical for gaseous worlds like Neptune, around these planets. In May 2016, the Hubble team observed the two innermost planets, and found no evidence for such puffy atmospheres. This strengthened the case that the planets closest to the star are rocky in nature.
Spitzer, Hubble, and Kepler will help astronomers plan for follow-up studies using NASA’s upcoming James Webb Space Telescope, launching in 2018. With much greater sensitivity, Webb will be able to detect the chemical fingerprints of water, methane, oxygen, ozone, and other components of a planet’s atmosphere. Webb also will analyze planets’ temperatures and surface pressures- key factors in assessing their habitability.
[https://exoplanets.nasa.gov/news/1419/nasa-telescope-reveals-largest-batch-of-earth-size-habitable-zone-planets-around-single-star/]
It is intriguing how different an extrasolar planetary system may be from our own, given the size of the planets, their distance from the host star, the faintness of the star, as well as the number of planets located in the habitable zone, in the previous case. But how many Earth-like exoplanets are found in the habitable zone of their star?
Of the more than 1,000 verified planets found by NASA’s Kepler Space Telescope, eight are less than twice Earth-size and in their stars’ habitable zone. All eight orbit stars cooler and smaller than our sun. The search continues for Earth-size habitable zone worlds around sun-like stars.
[https://www.nasa.gov/ames/kepler/nasa-keplers-hall-of-fame-small-habitable-zone-exoplanets]
Out of 1,000 verified planets, 8 of them are terrestrial and orbiting in the habitable zone of the host star. This is about 10%. Still in all 8 cases the stars are red dwarfs, much cooler than our own Sun. Supposing that no more than 20% of MS sequence stars are Sun-like (0.7-1.3 solar masses), this tells us that no more than 2% of terrestrial and habitable planets will be orbiting a Sun- like star in the Milky Way (so that they will be both Earth and solar analogs).
Of the previous terrestrial and habitable planets, the following are considered the most promising (as of 2015):
A 2015 review concluded that the exoplanets Kepler-62f, Kepler-186f and Kepler-442b were likely the best candidates for being potentially habitable. These are at a distance of 1,200, 490 and 1,120 light-years away, respectively. Of these, Kepler-186f is similar in size to Earth with a 1.2-Earth-radius measure and it is located towards the outer edge of the habitable zone around its red dwarf.
[https://en.wikipedia.org/wiki/List_of_potentially_habitable_exoplanets]
While Kepler-186 is a red dwarf, Kepler-62 and Kepler-442 are K-type stars (orange dwarfs).
[https://en.wikipedia.org/wiki/Kepler-62]
[https://en.wikipedia.org/wiki/Kepler-442]
Thus the closest Earth-like habitable planet orbiting a Sun- like star could be at least 500ly, probably more than 1,000ly, away.
2.3.3 Habitability outside the CHZ
The previous conclusion (which supports the Rare Earth hypothesis) may finally force us to adopt a different way of assessing the habitability of exoplanets, or even to reevaluate the meaning of an extraterrestrial ‘habitat.’
Here is the current attitude about the concept of the CHZ:
In subsequent decades, the concept of the CHZ began to be challenged as a primary criterion for life, so the concept is still evolving. Since the discovery of evidence for extraterrestrial liquid water, substantial quantities of it are now thought to occur outside the circumstellar habitable zone. The concept of deep biospheres, like Earth’s, that exist independently of stellar energy, are now generally accepted in astrobiology given the large amount of liquid water known to exist within the lithospheres and asthenospheres (the layer below the lithosphere) of planets in the Solar System. Sustained by other energy sources, such as tidal heating or radioactive decay or pressurized by non-atmospheric means, liquid water may be found even on rogue planets (planets ejected from the planetary system in which they formed), or their moons. Liquid water can also exist at a wider range of temperatures and pressures as a solution, for example with sodium chlorides in seawater on Earth, chlorides and sulphates on equatorial Mars, or ammoniates, due to its different colligative properties. In addition, other circumstellar zones, where non-water solvents favorable to hypothetical life based on alternative biochemistries could exist in liquid form at the surface, have been proposed.
Liquid-water environments have been found to exist in the absence of atmospheric pressure, and at temperatures outside the CHZ temperature range. For example, Saturn’s moons Titan and Enceladus and Jupiter’s moons Europa and Ganymede, all of which are outside the habitable zone, may hold large volumes of liquid water in subsurface oceans.
Outside the CHZ, tidal heating and radioactive decay are two possible heat sources that could contribute to the existence of liquid water. Abbot and Switzer (2011) put forward the possibility that subsurface water could exist on rogue planets as a result of radioactive decay-based heating and insulation by a thick surface layer of ice.
With some theorizing that life on Earth may have actually originated in stable, subsurface habitats, it has been suggested that it may be common for wet subsurface extraterrestrial habitats such as these to ‘teem with life.’ Indeed, on Earth itself living organisms may be found more than 6 kilometers below the surface.
Another possibility is that outside the CHZ organisms may use alternative biochemistries that do not require water at all. Astrobiologist Christopher McKay, has suggested that methane (CH4) may be a solvent conducive to the development of ‘cryolife,’ with the Sun’s ‘methane habitable zone’ being centered on 1,610,000,000 km (11 AU) from the star. This distance is coincident with the location of Titan, whose lakes and rain of methane make it an ideal location to find McKay’s proposed cryolife. In addition, testing of a number of organisms has found some are capable of surviving in extra-CHZ conditions.
The Rare Earth hypothesis argues that complex and intelligent life is uncommon and that the CHZ is one of many critical factors. According to Ward & Brownlee and others, not only is a CHZ orbit and surface water a primary requirement to sustain life but a requirement to support the secondary conditions required for multicellular life to emerge and evolve. The secondary habitability factors are both geological (the role of surface water in sustaining necessary plate tectonics) and biochemical (the role of radiant energy in supporting photosynthesis for necessary atmospheric oxygenation).
Species, including humans, known to possess animal cognition require large amounts of energy, and have adapted to specific conditions, including an abundance of atmospheric oxygen and the availability of large quantities of chemical energy synthesized from radiant energy. If humans are to colonize other planets, true Earth analogs in the CHZ are most likely to provide the closest natural habitat; this concept was the basis of Stephen H. Dole’s 1964 study. With suitable temperature, gravity, atmospheric pressure and the presence of water, the necessity of spacesuits or space habitat analogues on the surface may be eliminated and complex Earth life can thrive.
Planets in the CHZ remain of paramount interest to researchers looking for intelligent life elsewhere in the universe. The Drake equation, sometimes used to estimate the number of intelligent civilizations in our galaxy, contains the factor or parameter ne, which is the average number of planetary-mass objects orbiting within the CHZ of each star. A low value lends support to the Rare Earth hypothesis, which posits that intelligent life is a rarity in the Universe, whereas a high value provides evidence for the Copernican mediocrity principle, the view that habitability- and therefore life- is common throughout the Universe.
[https://en.wikipedia.org/wiki/Circumstellar_habitable_zone]
Thus, on one hand, we might say that if life could ‘thrive’ in subsurface water environments, or even be based on liquid methane (instead of liquid water), so that intelligent life might have evolved under such conditions on other planets of our solar system (or even on our own planet), we would already know it. On the other hand, the Rare Earth hypothesis, although it underlines the uniqueness of intelligent life as we know it, it does not exclude the appearance of life, either primitive or advanced, elsewhere in the universe, given the immense number of stars systems. For example, since it is estimated that about 10% of Earth-like planets is found in the habitable zone of a MS star in our Milky Way galaxy, if we suppose that in 10% of those planets life finally appeared, then, for a total of about 100 billion MS stars in the Milky Way, there could be as many as 1 billion Earth-like planets with life, of which 100 million will also be orbiting a Sun-like star. Therefore, if not abundant, Earth analogs may not be ‘rare’ after all.
Still at the time when mankind will have advanced enough to colonize other solar systems and their planets, the technology will also be sufficiently sophisticated to develop artificial environments. Thus habitability (in the sense of the CHZ) will not be the determining factor for settling on exoplanets. In fact technology could advance so much that artificial satellites orbiting exoplanets, or spaceships in the form of free-floating star-cities, may be considered. In such a sense, sufficiently advanced civilizations may not even depend on planets for their existence and sustenance.
[https://en.wikipedia.org/wiki/Timeline_of_the_evolutionary_history_of_life]
Although we haven’t yet discovered any form of life elsewhere, it seems that life appeared on the Earth very early:
The earliest time that life forms first appeared on Earth is unknown. The earliest known life forms on Earth are putative fossilized microorganisms found in hydrothermal vent precipitates. They may have lived earlier than 3.77 billion years ago, possibly as early as 4.28 billion years ago, not long after the formation of the Earth 4.54 billion years ago. A December 2017 report stated that 3.465-billion-year-old Australian Apex chert rocks once contained microorganisms, the earliest direct evidence of life on Earth. In January 2018, a study found that 4.5 billion-year-old meteorites found on Earth contained liquid water along with prebiotic complex organic substances that may be ingredients for life. According to biologist Stephen Blair Hedges, “If life arose relatively quickly on Earth … then it could be common in the universe.”
[https://en.wikipedia.org/wiki/Earliest_known_life_forms]
2.4.1 Abiogenesis
It seems that the protoplanetary disk from which are solar system was born already contained all the chemical elements along with liquid water and complex organic substances. These organic substances transformed later on into RNA and DNA molecules, in a process called abiogenesis:
Abiogenesis, or informally the origin of life, is the natural process by which life arises from non-living matter, such as simple organic compounds. The transition from non-living to living entities was not a single event but a gradual process of increasing complexity. Complex organic molecules have been found in the Solar System and in interstellar space, and these molecules may have provided starting material for the development of life on Earth. The biochemistry of life may have begun shortly after the Big Bang, 13.8 billion years ago, during a habitable epoch when the age of the universe was only 10 to 17 million years. The panspermia hypothesis alternatively suggests that microscopic life was distributed to the early Earth by space dust, meteoroids, asteroids and other small Solar System bodies and that life may exist throughout the Universe. The panspermia hypothesis proposes that life originated outside the Earth, not how life came to be. Nonetheless, Earth remains the only place in the Universe known to harbor life.
[https://en.wikipedia.org/wiki/Abiogenesis]
The ease with which life in the form of RNA and DNA molecules appears from basic organic and inorganic elements was demonstrated by the Miller-Urey experiment:
The Miller- Urey experiment was a chemical experiment that simulated the conditions thought at the time to be present on the early Earth, and tested the chemical origin of life under those conditions.
The experiment used water (H2O), methane (CH4), ammonia (NH3), and hydrogen (H2). The chemicals were all sealed inside a sterile 5-liter glass flask connected to a 500 ml flask half-full of liquid water. The liquid water in the smaller flask was heated to induce evaporation, and the water vapor was allowed to enter the larger flask. Continuous electrical sparks were fired between the electrodes to simulate lightning in the water vapor and gaseous mixture, and then the simulated atmosphere was cooled again so that the water condensed and trickled into a U-shaped trap at the bottom of the apparatus.
After a day, the solution collected at the trap had turned pink in color. At the end of one week of continuous operation, the boiling flask was removed, and mercuric chloride was added to prevent microbial contamination. The reaction was stopped by adding barium hydroxide and sulfuric acid, and evaporated to remove impurities. Using paper chromatography, Miller identified five amino acids present in the solution: glycine, α-alanine and β-alanine were positively identified, while aspartic acid and α-aminobutyric acid (AABA) were less certain, due to the spots being faint.
After Miller’s death in 2007, scientists examining sealed vials preserved from the original experiments were able to show that there were actually well over 20 different amino acids produced in Miller’s original experiments. That is considerably more than what Miller originally reported, and more than the 20 that naturally occur in life. More recent evidence suggests that Earth’s original atmosphere might have had a composition different from the gas used in the Miller experiment. But prebiotic experiments continue to produce racemic mixtures (containing both L and D enantiomers) of simple to complex compounds under varying conditions. However, in nature, L amino acids dominate. Later experiments have confirmed disproportionate amounts of L or D oriented enantiomers are possible.
[https://en.wikipedia.org/wiki/Miller%E2%80%93Urey_experiment]
2.4.2 The problem of homochirality
Homochirality refers to the property of a group of molecules that possess the same chirality. It is an important feature of terrestrial biochemistry. All life on Earth is homochiral (with rare exceptions); only L-amino acids are encoded in proteins, and only D-sugars form the backbones of DNA and RNA.
[http://link.springer.com/referenceworkentry/10.1007%2F978-3-642-11274-4_731]
The aspect that in experiments both L and R enantiomers of the amino acids are produced, while in nature L amino acids dominate, has been used as an argument against the self-sufficiency of life and in favor of intelligent design:
Homochirality is essential to the correct functioning of many of the mechanisms of contemporary life-forms. But how did it arise in the first place? In order for homochiral macro-molecules to have evolved there must have been a mechanism which could discriminate between the molecular sub-units from their mirror images, and construct the macro-molecules from the sub-units of correct chirality. In contemporary life-forms this is done using complex mechanisms in which highly evolved (homochiral) molecules perform key functions. Clearly such highly evolved molecules would not have been available from the outset. We must therefore ask: What was the origin of chiral discrimination?
To date, there is no generally accepted answer to this question. Noam Lahav indicates that the organic chemist William Bonner argued at a meeting in the mid 1990’s that there was a big gap between the origin of homochirality and the origin of life, and that homochirality must have preceded life. Bonner has suggested an extraterrestrial source for homochiral molecules. Others, including Stanley Miller and Jeffrey Bada have argued that homochirality is an ‘artefact of life’ rather than a precondition.
[http://www.simsoup.info/Origin_Issues_Homochirality.html]
2.4.3 Life is abundant
The problem of homochirality is of the same nature as the problem of baryon asymmetry (the imbalance of matter and antimatter in the observable universe). An even more fundamental mechanism is called spontaneous symmetry breaking, a process by which a physical system in a symmetric state ends up in an asymmetric state:
Chiral symmetry breaking is an example of spontaneous symmetry breaking affecting the chiral symmetry of the strong interactions in particle physics. It is a property of quantum chromodynamics, the quantum field theory describing these interactions, and is responsible for the bulk of the mass (over 99%) of the nucleons, and thus of all common matter. It served as the prototype and significant ingredient of the Higgs mechanism underlying the electroweak symmetry breaking.
[https://en.wikipedia.org/wiki/Spontaneous_symmetry_breaking#Chiral_symmetry]
Thus ‘divine intervention’ is not necessary in order to explain the appearance of life and the evolution of primitive lifeforms into intelligent beings, if spontaneity is another perquisite of intelligence. Therefore, taking into account abiogenesis, the appropriate statement will be ‘Life is abundant.’
Another interesting aspect with respect to the possible abundance of life out there, is the following one. If some advanced technological civilizations exist in the Milky Way, then the ratio with which life appears on other planets by terraforming, can be significantly higher than what would be by natural processes. Therefore if the frequency fl in Drake’s equation is high on its own, it may even be higher due to the presence of advanced civilizations. But if such civilizations existed, the frequency fi might also be higher, by genetically engineering primitive species on other planets. If it is for the benefit of an advanced civilization to come in contact with a less advanced civilization, then the hypothesis of advanced civilizations is falsified by the mere fact that we have never been contacted. On the other hand, if such a contact has disastrous effects on the less advanced civilization, due to culture shock, then the existence of advanced civilizations out there is still possible, although it cannot be proved or rejected.
2.4.4 Selective destruction
A possible mechanism to explain homochirality on a cosmological scale is supernova explosions:
Vela Supernova Remnant
[https://apod.nasa.gov/apod/ap150101.html]
A near-Earth supernova is an explosion resulting from the death of a star that occurs close enough to the Earth (roughly less than 10 to 300 parsecs (30 to 1000 light-years) away to have noticeable effects on the Earth’s biosphere.
On average, a supernova explosion occurs within 10 parsecs (33 light-years) of the Earth every 240 million years. Gamma rays are responsible for most of the adverse effects a supernova can have on a living terrestrial planet. In Earth’s case, gamma rays induce a chemical reaction in the upper atmosphere, converting molecular nitrogen into nitrogen oxides, depleting the ozone layer enough to expose the surface to harmful solar and cosmic radiation (mainly ultra-violet). Phytoplankton and reef communities would be particularly affected, which could severely deplete the base of the marine food chain.
Speculation as to the effects of a nearby supernova on Earth often focuses on large stars as Type II supernova candidates. Several prominent stars within a few hundred light years of the Sun are candidates for becoming supernovae in as little as a millennium. Although they would be spectacular to look at, were these ‘predictable’ supernovae to occur, they are thought to have little potential to affect Earth.
Evidence from daughter products of short-lived radioactive isotopes shows that a nearby supernova helped determine the composition of the Solar System 4.5 billion years ago, and may even have triggered the formation of this system. Supernova production of heavy elements over astronomic periods of time ultimately made the chemistry of life on Earth possible.
[https://en.wikipedia.org/wiki/Near-Earth_supernova]
It has even been supposed that the major Ordovician-Silurian extinction events of 450 million years ago may have been caused by a GRB (gamma-ray burst).
[https://en.wikipedia.org/wiki/Gamma-ray_burst#Rate_of_occurrence_and_potential_effects_on_life]
However it has also been suggested that supernovae may also responsible for the chirality of the biological molecules, in a process called selective destruction:
A longstanding puzzle in biology and astrobiology has been the existence of left-handed amino acids and the virtual exclusion of their right-handed forms. This is especially puzzling because most mechanisms suggested for creating this ‘enantiomerism’ would create one form in nature locally but would create equal numbers of the other somewhere else. The total dominance of the left-handed forms on Earth is well known, but the left-handed forms appear also to be preferred beyond the locality of Earth, based on meteoritic evidence.
It is generally accepted that if some mechanism can introduce an imbalance in the populations of the left- and right-handed forms of any amino acid, successive synthesis or evolution of the molecules may amplify this enantioenrichment to produce ultimately a single form. What is not well understood, though, is the mechanism by which the initial imbalance can be produced, and the means by which it always produces the left-handed chirality for the amino acids.
One suggested mechanism lies with processing of a population of amino acids, or of their chiral precursors, by circularly polarized light; this could select one chirality over the other. However, this solution does not easily explain why it would select the same chirality in every situation, as is apparently observed (albeit with limited statistics), or why the physical conditions that would select one form in one place would not select the other in a different location.
Another possibility invoked selective processing by some manifestation of the weak interaction, which does violate parity conservation, so might perform a selective processing. This idea was based on earlier work focused on the β-decay of 14C to produce the selective processing. However, it was not possible in that study to show how simple β-decay could produce chiral-selective molecular destruction. A modern update on this possibility appears to produce some enantioenrichment.
Another suggestion assumed that neutrinos emitted by a core-collapse supernova would selectively process the carbon or the hydrogen in the amino acids to produce enantiomerism. This suggestion also did not explain how a predisposition toward one or the other molecular chirality could evolve from the neutrino interactions. A similar suggestion involves the effects of neutrinos from supernovae on molecular electrons.
Two features of supernovae are important: the magnetic field that is established as the star collapses to a neutron star or a black hole and the intense flux of neutrinos that is emitted as the star cools. The magnetic fields only have to couple to the molecules strongly enough to produce some orientation of their non-spin-zero nuclei. However, the 14N must also couple in some way to the molecular chirality. In the model we assume to describe this, the neutrinos preferentially interact with the 14N atoms in one of the chiral forms, and convert the 14N to 14C, thereby destroying that molecule and so preferentially selecting the other chiral form.
Another question involves the extent to which a single chirality might populate the entire Galaxy. Although supernovae could not do so by themselves, subsequent chemical amplification of the chirality-selected, biologically-interesting molecules would amplify the enantiomerism of the dominant form. Then Galactic mixing, operating on a slower timescale, would be able to establish the dominant form throughout the Galaxy. These two mechanisms would make it likely that the Galaxy would be populated everywhere with the same preferred chiral form.
If this model turns out to be correct, the longstanding question of the origin of the organic molecules necessary to create and sustain life on Earth will have undergone a strong suggestion that the processes of the cosmos played a major role in establishing the molecules of life on Earth, either directly, or by providing the seeds that ultimately produced homochirality in the amino acids. These molecules would appear to have been created in the molecular clouds of the galaxy, with their enantiomerism determined by supernovae, and subsequently either transported to Earth only in meteorites, swept up as the Earth passed through molecular clouds, or included in the mixture that formed Earth when the planets were created.
[http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3131570/]
If the chirality of organic molecules was already decided in the early stages of our planetary system by a supernova catalyst, since the L-enantiomers are also present in meteors, then a supernova explosion or generally a gamma-ray burst may have also been responsible for the emergence of complex intelligent life, through a series of beneficial DNA mutations triggered by the radiation. Even indirectly, if for example mass extinction events can be caused by supernova explosions or gamma-ray bursts, such events may determine evolutionary life-cycles, during which a species has the opportunity to evolve and advance, before it is replaced by another more sophisticated species. Furthermore, the range within which a supernova is effective but not devastating may be significant, so that even if life in the form of the appropriate biological molecules is abundant in the universe, the chances for the emergence of intelligent life could be limited.
While life in a primitive form appeared on the Earth very early, just half a billion years after the planet formed, it took almost 4.5 billion years (which is about equal to the whole lifetime of the planet) for intelligent life to emerge, in the form of humans beings, who pose questions about the origin of life, and are perhaps intelligent enough to question their own intelligence. Thus while probiotic life may be common in the universe, intelligent life may be unique. But does this uniqueness imply the sparsity of intelligent beings in the universe, or the variety of forms in which intelligence may appear?
2.5.1 Defining intelligence
This is the definition of intelligence according to Google search:
-The ability to acquire and apply knowledge and skills.
-The collection of information of military or political value.
[https://www.google.gr/search?q=intelligence]
This is the related article of Wikipedia:
Intelligence has been defined in many different ways including as one’s capacity for logic, understanding, self-awareness, learning, emotional knowledge, reasoning, planning, creativity, and problem solving. It can be more generally described as the ability or inclination to perceive or deduce information, and to retain it as knowledge to be applied towards adaptive behaviors within an environment or context.
Intelligence is most widely studied in humans, but has also been observed in non-human animals and in plants. Artificial intelligence is intelligence in machines. It is commonly implemented in computer systems using program software.
The definition of intelligence is controversial. Psychology and learning researchers have suggested definitions of intelligence such as (Alexander Wissner-Gross):
“Intelligence is a force F, which acts so as to maximize future freedom of action, or keep options open, with some strength T, with the diversity of possible accessible futures S, up to some future time horizon, τ. In short, intelligence doesn’t like to get trapped.”
[https://en.wikipedia.org/wiki/Intelligence]
For me, intelligence could be identified with the degrees of freedom n available to a system of information I. The degrees of freedom would correspond to the different ways intelligence can deal with the information available. Commonly information is given as the logarithm (either decimal or natural) of the degrees of freedom,
The entropy S of a system is proportional to its informational context,
where kB is Boltzmann’s constant.
Intelligence in turn can be related to the degrees of freedom n by setting,
where we may call the factor Γ, free will.
In order to introduce the physical notion of energy E, we may suppose that information can be given in relation to the energy of the system (instead of the degrees of freedom n),
so that the total energy of the system E0 can be expressed in relation to its informational content plus the degrees of freedom of the system,
Setting
we take
where we may call the constant 𝒞 consciousness.
In fact the constant 𝒞 is a constant of integration, which stems from an equation of exponential growth,
A time dependent expression can be derived by substituting
where γ will be the growth factor.
I did the previous calculations in order to suggest a possible way by which an extraterrestrial civilization might be detected by its entropy S imprint, in relation to the energy E the civilization consumes,
This way the intelligence of a civilization might also be measured, by how fast that civilization grows on its own free will Γ,
2.5.2 Intelligent life is unique
An interesting thought is the following one: Does life presupposes intelligence? Does intelligence presupposes life? On one hand, we may say that if something is living then it must also be intelligent, as it has to find ways to ensure its survival and continuation. From there after, we can distinguish between primitive and advanced lifeforms. On the other hand, we may also regard artificial intelligence as a form of intelligence, although in this case a ‘smart computer’ is not something living. Or is it? If the criterion of life is basically survival and perpetuation, then artificial intelligence could advance at such a level that machines (robots) might also learn how to replicate themselves and survive, probably at the expense of human beings.
It has also been suggested that in the future biology (humans) and artificial intelligence (machines) could merge to create a new hybrid species, while the distinction between what is natural and what is artificial will have lost any meaning. If evolution is all about ‘survival of the fittest,’ a cyborg organism will certainly have the advantage, combining the mentality of the human nature, with the computing power of a machine. Such an aspect also makes us wonder about the nature of advanced extraterrestrial intelligence. Will they be ‘human-like,’ so that we could establish some compatible form of communication, or will they be ‘robot-like,’ so that an emotion-based language like ours will be meaningless to them? Perhaps AI (artificial intelligence) is all about improving the human nature, so that machines will finally become a supplement (instead of a substitute) to human weakness. In that sense the definition of intelligence will always revolve around the purpose and meaning of the human condition.
Therefore we might say that although primitive (microbial) life can be abundant in the universe, intelligent life may be unique. But by this uniqueness it is not meant that intelligent life is necessarily sparse. More appropriately we should consider that extraterrestrial intelligence might be very different from what we commonly refer to or understand as ‘intelligent.’ In that sense, as the Earth analog, so the ‘human analog’ may be rare out there.
If intelligent life is rare out there, the possibility of communication will be rather remote, as the distances separating those few intelligent species in the Milky Way will be forbidding. But how far our radio signals can reach? This is a dialogue which I found on the internet:
Question:
“Could you please give me an indication of how far away we could detect a civilization with Earth-like technology? That is, if there were a society with radio, television, radar, etc., transmission power at a level equal to our own, radiating from omnidirectional antennas on an Earth-like planet, what would be the maximum distance in lightyears that we could detect these signals with our current SETI receiver sensitivity?”
Answer:
“My calculations indicate that incidental radiation from Earth-like technology could be detected out to at least 1000 LY (light years) by our larger SETI telescopes (such as the ones used in the SETI Institute’s Project Phoenix targeted search). Since our members’ own privately owned and operated radio telescopes are much smaller and less sensitive, it is unlikely that we would be able to detect such incidental radiation from any but the very nearest stars. For example, a one Megawatt transmitter driving a 100 meter diameter antenna can be detected by the typical amateur SETI station at a distance of 1 parsec, which is slightly less than the distance to the nearest star. The actual range over which we can hear a signal depends upon the transmit power and antenna gain of the civilization we are trying to detect- factors over which we have no control whatever. Our private search hopes to encounter either significantly more powerful transmissions, or highly directional beacons. Thus the two approaches (sky survey and targeted search) are complementary.
[http://www.setileague.org/askdr/howfar.htm]
Probably the range of 1,000ly suggested by the previous answer is too optimistic. In fact random radio transmissions, such as TV signals, do not travel more than a couple of light years, before they become noise:
The reach of TV signals
In the movie Contact, astronomers receive a radio signal from the star Vega. Buried within the signal is a broadcast of Hitler’s speech for the opening of the 1936 Olympic Games. The television signal had made the 25 light year journey to Vega, which let the aliens know we’re here. The idea that our television and radio signals are gradually reaching ever more distant stars is a popular one, but in reality things aren’t so simple.
The opening ceremony of the 1936 Olympics was the first major television signal at a frequency high enough to penetrate Earth’s ionosphere. From there you could calculate that any star within about 80 light years of Earth could detect our presence. There’s even a website that shows which TV shows might be reaching potentially habitable worlds. But the problem with this idea is that it isn’t good enough for the signal to reach a distant star, it also needs to be powerful and clear enough to be detectable.
For example, the most distant human-made object is Voyager I, which has a transmission power of about 23 Watts, and is still detectable by radio telescopes 125 AU away. Proxima Centauri, the closest star to the Sun, is about 2,200 times more distant. Since the strength of a light signal decreases with distance following the inverse square relation, one would need a transmission power of more than 110 million Watts to transmit a signal to Proxima Centauri with the strength of Voyager to Earth. Current TV broadcasts is limited to around 5 million Watts for UHF stations, and many stations aren’t nearly that powerful.
One might argue that an advanced alien civilization would surely have more advanced detectors than we currently have, so a weaker signal isn’t a huge problem. However the television signals we transmit aren’t targeted at space. Some of the signal does leak out into space, but they aren’t specifically aimed at a stellar target the way Voyager I’s signal is aimed at Earth. They also lack a clear mechanism for how transform the signal to an image. On Earth this works by implementing a specific standard, which any alien civilization would need to reverse engineer to really watch TV. On top of that, there is the problem of scattering and absorption of the signal by interstellar gas and dust. This can diminish the power and distort the signal. Even if aliens could detect our signals, they might still confuse it with background noise.
That doesn’t mean it’s impossible to communicate between stars. It just means that communication would require an intentional effort on both sides. If you really want to communicate with aliens, you need to make sure your signal is both clear and readable. To make it stand out among all the electromagnetic noise in the universe, you’d want to choose a wavelength were things are relatively quiet. You also need to make your signal easy to recognize as an artificial signal. In Contact the aliens did this by transmitting a series of prime numbers.
In 1974 humanity made its most famous effort to send a signal to the stars. It was a radio transmission sent from the Arecibo observatory, and consisted of 1,679 binary digits, lasting three minutes. Since 1,679 is the product of the primes 23 and 73, the bits can be arranged into an image of those dimensions. There have been other efforts to send messages to the stars, but they haven’t been as powerful or as simple.
Beyond a few light years, our leaky TV broadcasts are likely undetectable. As we’ve switched to digital television and lower transmission powers they’ve become even harder to detect. Any aliens looking for us will have to rely on other bits of evidence, such as the indication of water in our atmosphere or chlorophyll on Earth’s surface, just as we will strive to detect such things on distant worlds. Either way, the first message received won’t be a complex text of information. It will simply be a recognition of life on another world.
[https://briankoberlein.com/2015/02/19/e-t-phone-home/]
Thus it is possible that we wouldn’t be able to detect radio signals, even if such signals were transmitted by a civilization located in the nearest solar system, Alpha Centauri, which is about 4ly away from us. Additionally, as our technology improves, the more civilizations we might trace, the less civilizations might trace us, as the more our technology advances, the stealthier it may become. Furthermore the timespan during which a civilization uses radio transmissions as we know them may be limited, in the sense that, after this period, more advanced methods of communication may be used, unknown to us at present. Thus there is a narrow window of space and time available to civilizations, who are approximately at the same evolutionary stage, to communicate. Still the basic problem seems to be that communication has to be targeted. By ‘targeted’ it is implied both that telescopes have to be powerful enough and also that we are sincerely willing to communicate. But perhaps while we expect to receive targeted and meaningful signals from an extraterrestrial civilization, at the same time we may avoid sending similar signals to outer space, because of the possible consequences of been detected, if for example those who detect us are hostile and have the technology to come here. Therefore with respect to the probability of communication fc in Drake’s equation, the willingness to communicate is an additional aspect to be considered.
2.5.5 Timeline of intelligent life
While there is no data or evidence indicating the presence of any extraterrestrial civilization other than our own, this is a way to make an indirect estimation about the frequencies fl, fi, and fc, in Drake’s equation, in comparison to the Earth’s own history. For this purpose we may consider the time when some critical events took place on the Earth with respect to the appearance of life, humans, civilizations, and advanced civilizations, and compare this time to the Earth’s age:
Thus the frequency fl, the percentage of habitable planets with life, will be high, close to 1. This is supported by the fact that microbial life appeared very early in Earth’s history, and was also very persistent, defying mass extinction events. The frequency fi, referring to the percentage of intelligent species, was chosen to correspond to Homo Sapiens (anatomically modern humans). The frequency fc, corresponding to the percentage of civilizations with radio transmissions, is very close to the percentage of modern (industrialized) civilizations, since the timespan between the Industrial Revolution and the Modern Era is relatively very small, compared to the Earth’s age.
Such results, which indeed may not be very far from the true percentages, are suggestive of the orders of magnitude separating the different stages. While the probability of life appearing on an Earth-like habitable planet may be close to 1, the presence of an intelligent species on this planet is much less probable, while the probability of a civilization able to communicate with radio signals is even smaller.
It has been assumed that the number L in Drake’s equation is the most important parameter:
Returning now to Drake’s equation,
where the number j counts the frequencies (first frequency fp, j=1, second frequency en, j=2, etc.).
Apart from this, if we set
we take
In that sense the easiest way to treat Drake’s equation is to write
2.6.1 Life expectancy
This is similar to calculating the life expectancy of a human being:
According to this data, the average human life expectancy in 2006 was
2.6.2 Extinction event
It is interesting to note that the maximum life expectancy has more or less been constant:
Such syllogisms are related to what is commonly referred to as a mass extinction:
2.6.3 Our closest neighbors
This is a list of stars within a range of about 15ly:
This is a wider range of stars within a radius of 50y:
The closest exoplanet to our solar system is Proxima Centauri b:
List of exoplanets in the conservative habitable zone:
[https://en.wikipedia.org/wiki/List_of_potentially_habitable_exoplanets]
This is a table with some possible frequencies:
2.7 Number of civilizations
The L term is considered the most important one in Drake equation. We have no idea how long a technological civilization can last. Even if only one extraterrestrial civilization lasts for billions of years, or becomes immortal, the L factor would be enough to reduce Drake’s equation to N = L. Actually, Frank Drake recognizes this in his license plate.
[http://www.astrobio.net/news-exclusive/at-last-how-many-alien-civilizations-are-there/]
My own logic tells me that if there is just one super- advanced civilization in the Milky Way, so advanced that they have already colonized the whole Milky Way, then the number of civilizations in Drake’s equation will be equal to N=1, because there will be exactly 1 ‘empire’ in the Milky Way. However such an assumption is falsified by the evidence: such an empire does not exist, as we know it. Still the number N at the moment is indeed equal to 1, because we are the only civilization in the Milky Way which we can account for right now.
Returning now to Drake’s equation,
a compact expression can be taken by representing the product of the frequencies in the following way
where the number j counts the frequencies (first frequency fp, j=1, second frequency en, j=2, etc.).
The frequency en in fact estimates the number of planets which are habitable, so that we may also call it fh.
Apart from this, if we set
we take
Thus the number N of civilizations will be proportional to the number L. However the constant k will have units of R* stars per year (since the frequencies fj are percentages thus dimensionless). Therefore, since L has units of years, what truly N counts is number of stars.
where N* will be the total number of stars, and the number L* will be the lifespan of a star instead of a civilization. This way we avoid the problem of estimating the lifespan of a civilization (which is highly speculative) all together.
2.6.1 Life expectancy
The number N* of stars in the Milky Way can be estimated if we know the production rate R* of stars and their average lifespan L*. Vice versa, we can estimate the life expectancy of a star if we know the number of stars and their production rate. For example if we account for a total of N*=100 billion stars, and we assume a growth rate of R*=1 star per year, the average life expectancy of a star will be
As we have already seen, this lifespan corresponds to the average MS star of mass 0.4 M☉ (solar masses).
This is similar to calculating the life expectancy of a human being:
The average global birth rate is 18.6 births per 1,000 total population in 2016. The death rate is 7.8 per 1,000 per year. The RNI (rate of natural increase) is thus 1.06 percent. The 2016 average of 18.6 births per 1,000 total population is estimated to be about 4.3 births/second or about 256 births/minute for the world.
[https://en.wikipedia.org/wiki/Birth_rate]
The world population was estimated to have reached 7.6 billion as of December 2017. (As of March 2016, the human population was estimated at 7.4 billion.) The 2012 UN (United Nations) projections show a continued increase in population in the near future with a steady decline in population growth rate. The United Nations estimates it will further increase to 11.2 billion in the year 2100.
Some analysts have questioned the sustainability of further world population growth, highlighting the growing pressures on the environment, global food supplies, and energy resources.
[https://en.wikipedia.org/wiki/World_population]
According to this data, the average human life expectancy in 2006 was
In the previous calculations it was assumed that the rate R refers to the new births. A more accurate result can be obtained taking into account that population growth is generally exponential or logistic.
As far as our discussion is concerned, it is interesting to note that the projected maximum number of people is approximately equal to the estimated number of Sun-like stars in the Milky Way galaxy (10 billion). Presumably if we only account for Sun-like stars (stars with a mass close to the mass of the Sun, excluding thus low mass red dwarfs), and supposing that, more or less, all of them have an Earth-like habitable planet, then the maximum possible number of civilizations in those star systems will be 10 billion (equal to the number of the Sun-like stars). If we also include red dwarfs (increasing thus the number of possible habitable star systems to 100 billion), there could me as many as 100 billion civilizations in the Milky Way. Still if we assume that an advanced civilization occupies an area of at least 10ly, containing on average about 10 star systems, then the maximum expected number of civilizations will be 10 billion. Of course all this will allegedly take place in the distant future, when advanced civilizations will have the ability to occupy any available star system, by terraforming and colonizing it. At that hypothetical stage (assuming an equilibrium where the birth rate of civilizations is equal to the death rate, R=1) the life expectancy of civilizations L will be equal to the number of civilizations N.
2.6.2 Extinction event
The fossil record reveals a general increase in the diversity of organisms over time, interrupted by periodic mass extinctions. Five mass extinctions occurred at the end of the Ordovician, Devonian, Permian, Triassic, and Cretaceous periods. The Permian mass extinction was the most severe.
[http://bio1152.nicerweb.com/Locked/media/ch25/extinctions.html]
According to Wikipedia, it is estimated that of the roughly 150,000 people who die each day across the globe, about two thirds- 100,000 per day- die of age- related causes. In industrialized nations the proportion is much higher, reaching 90%.
[https://en.wikipedia.org/wiki/Cause_of_death]
Worldwide, the average life expectancy at birth was 71.0 years over the period 2010- 2013 according to United Nations World Population Prospects 2012 Revision.
[https://en.wikipedia.org/wiki/List_of_countries_by_life_expectancy]
However this data may be far from true in reality, if we include infant mortality all around the globe, and if consider much larger time scales. This is another article of Wikipedia about life expectancy:
Life expectancy is a statistical measure of the average time an organism is expected to live, based on the year of their birth. 17th-century English life expectancy was only about 35 years, largely because infant and child mortality remained high. Life expectancy was under 25 years in the early Colony of Virginia, and in seventeenth-century New England, about 40 per cent died before reaching adulthood. (Currently) human beings are expected to live on average 30- 40 years in Swaziland and 82.6 years in Japan, but the latter’s recorded life expectancy may have been very slightly increased by counting many infant deaths as stillborn. Life expectancy increases with age as the individual survives the higher mortality rates associated with childhood.
[https://en.wikipedia.org/wiki/Life_expectancy]
If we compare the life expectancy in third world countries (35 years in Swaziland) to that in advanced countries (83 years in Japan), the average does not add up to 70 years but it is lower (about 60 years at best). Even so, according to the same data, life expectancy was approximately constant from the Paleolithic, through the Middle Ages, and more or less until the 20th century, and equal to about 25-30 years.
Furthermore life expectancy refers to the average human lifespan, not to its maximum possible value:
Maximum life span (or, for humans, maximum reported age at death) is a measure of the maximum amount of time one or more members of a population have been observed to survive between birth and death, provided circumstances that are optimal to that member’s longevity. Most living species have at least one upper limit on the number of times the cells of a member can divide. This is called the Hayflick limit, although number of cell divisions does not strictly control lifespan. No fixed theoretical limit to human longevity is apparent today. A theoretical study suggested the maximum human lifespan to be around 125 years. The longest-living person whose dates of birth and death were verified was Jeanne Calment (1875-1997), a French woman who lived to 122.
[https://en.wikipedia.org/wiki/Maximum_life_span]
It is interesting to note that the maximum life expectancy has more or less been constant:
The Centers for Disease Control and Prevention, recently had some good news: The life expectancy of Americans is higher than ever, at almost 78. Discussions about life expectancy often involve how it has improved over time. According to the National Center for Health Statistics, life expectancy for men in 1907 was 45.6 years; by 1957 it rose to 66.4; in 2007 it reached 75.5.
Unlike the most recent increase in life expectancy (which was attributable largely to a decline in half of the leading causes of death including heart disease, homicide, and influenza), the increase in life expectancy between 1907 and 2007 was largely due to a decreasing infant mortality rate, which was 9.99 percent in 1907; 2.63 percent in 1957; and 0.68 percent in 2007. But the inclusion of infant mortality rates in calculating life expectancy creates the mistaken impression that earlier generations died at a young age; Americans were not dying en masse at the age of 46 in 1907.
The fact is that the maximum human lifespan- a concept often confused with ‘life expectancy’- has remained more or less the same for thousands of years. The idea that our ancestors routinely died young (say, at age 40) has no basis in scientific fact. When Socrates died at the age of 70 around 399 B.C., he did not die of old age but instead by execution. It is ironic that ancient Greeks lived into their 70s and older, while more than 2,000 years later modern Americans aren’t living much longer.
[http://www.livescience.com/10569-human-lifespans-constant-2-000-years.html]
If by analogy we consider that the life expectancy of civilizations who may exist in the universe can be compared to the average human life expectancy, we take the following ratios:
Thus we may say that just a quarter of primitive species in the universe survive to an advanced stage, while about half of those species who advance reach a mature stage.
Such syllogisms are related to what is commonly referred to as a mass extinction:
An extinction event (also known as a mass extinction or biotic crisis) is a widespread and rapid decrease in the biodiversity on Earth. Such an event is identified by a sharp change in the diversity and abundance of multicellular organisms. It occurs when the rate of extinction increases with respect to the rate of speciation. Because most diversity and biomass on Earth is microbial, and thus difficult to measure, recorded extinction events affect the easily observed, biologically complex component of the biosphere rather than the total diversity and abundance of life.
Extinction occurs at an uneven rate. Estimates of the number of major mass extinctions in the last 540 million years range from as few as five to more than twenty. These differences stem from the threshold chosen for describing an extinction event as ‘major,’ and the data chosen to measure past diversity.
[https://en.wikipedia.org/wiki/Extinction_event]
If we account for a number of 20 extinction events in the last 500 million years, this would give us an average cosmic cycle of 10 million years. A cosmic cycle can be defined as the average timespan during which a species is given the opportunity to appear and evolve, as much as to avoid its destruction at the end of the cycle. The character and duration of such cycles can be identified with events either physical, terrestrial (e.g. plate tectonics) or extraterrestrial (e.g. comets, supernovae, etc.); or artificial (if the extinction event is caused by the same species).
At present the rates at which the humankind advances are much greater than any cosmic cycle, given the large timespan of such a cycle. Still, even though right now a large meteor could hit the Earth, or a large volcano could erupt, and without us been able to do anything about it, it seems that the greatest environmental danger at present is ourselves. This has made many people talking about a 6th mass extinction:
The Holocene extinction, otherwise referred to as the Sixth extinction or Anthropocene extinction, is the ongoing extinction event of species during the present Holocene epoch, mainly as a result of human activity. The large number of extinctions spans numerous families of plants and animals, including mammals, birds, amphibians, reptiles and arthropods. With widespread degradation of highly biodiverse habitats such as coral reefs and rainforest, as well as other areas, the vast majority of these extinctions is thought to be undocumented. The current rate of extinction of species is estimated at 100 to 1,000 times higher than natural background rates.
Various species are predicted to become extinct in the near future, among them the rhinoceros, nonhuman primates, pangolins, and giraffes. Hunting alone threatens bird and mammalian populations around the world. Some scientists and academics assert that industrial agriculture and the growing demand for meat is contributing to significant global biodiversity loss as this is a significant driver of deforestation and habitat destruction; species-rich habitats, such as significant portions of the Amazon region, are being converted to agriculture for meat production. According to the WWF’s 2016 Living Planet Index, global wildlife populations have declined 58% since 1970, primarily due to habitat destruction, over-hunting and pollution. They project that if current trends continue, 67% of wildlife could disappear by 2020. 189 countries, which are signatory to the Convention on Biological Diversity (Rio Accord), have committed to preparing a Biodiversity Action Plan, a first step at identifying specific endangered species and habitats, country by country.
[https://en.wikipedia.org/wiki/Holocene_extinction]
Perhaps the search for extraterrestrial intelligence on other planets is nothing else than our journey towards the realization of how important our own planet is, and how stupid we have been (including all of us) searching for the possibility of life elsewhere (while life had already been abundant here).
Whatever caused the extinction of the dinosaurs, many people believe that the reason we are here is because dinosaurs disappeared. But this may be far from true. In fact we are the descendants of mammalian reptiles, which co-existed with dinosaurs. The Permian extinction (250 million years ago) could have been the cause that dinosaurs prevailed over the mammalian reptiles. If this is true, then mass extinctions do not promote life, but set life back, whatever the lifeforms may be. Therefore mass extinctions had better be seen as drawbacks in evolution, even if they act as mechanisms of natural selection.
Given this, is it interesting to wonder if on some other planet some exospecies was luckier not to have been hit by a major catastrophe the last 250 million years. If such a planet is of about the same age as our own planet, and life there appeared about at the same time as on the Earth, then such lifeforms may have advanced much more than us. On the other hand, the persistence of life on the Earth suggests that even if mass extinctions occur from time to time, it seems that life finds ways to survive, so that the determining factor for the advancement of intelligent life may finally be time itself. For example, if some disturbance caused by a major catastrophe lasts a couple of million years, and 5 such big disasters have taken place in the Earth’s history the last 500 million years, then the total time of disruption will be 10 million years, just 2% for a total of 500 million years.
Dinosaurs were thriving on the planet for about 200 million years before they disappeared, 65 million years ago. One might say that they had had at their disposal all the time in the world to evolve, but they didn’t. Why is that? Were they stupid? Were mammalian reptiles (from which we evolved) also stupid not to replace the dinosaurs in time (after the Permian extinction)? Are we stupid because of the fact that if a comet hits us right now, or if we experience a series of major volcanic eruptions which will poison our planet, we will be unable to react? They only viable and certain solution against such a possibility is to settle on another planet, so that we will survive even if our planet is destroyed. But how much is it really worth if we are forced to settle on another planet because we have destroyed the Earth? Could we say that the Anthropocene extinction is an inescapable consequence of progress? Or that the term ‘Anthropocene’ implies that humans, at least as we know them right now, will disappear too?
It is possible that only few species in the universe advance at a level beyond the point of self- destruction. This point is also related to the notion of the technological singularity. The human species has been exhibiting a persistent tendency not to learn from the mistakes of the past (thus there is some insufficient memory capacity), as well as to enjoy tormenting and killing other species, including its own kind (thus here is also some mental inability or even instability to overcome animal instincts). If someone says that gradually we will get better, this is just wishful thinking, because, in all likelihood, there are some truly advanced species out there, which, both spiritually and technologically, due to favored conditions, have always been better, so that they really deserve to inherit the universe. This is not to say that we should stop making progress and search for those better species. But it is good to know the limits of what we can learn, and how far our advancement can reach.
Our Sun will die in about 5 billion years. At the same time it is believed that our Milky Way galaxy will collide with the Andromeda galaxy. Even more, as current observations suggest, if the universe is right now at a state of equilibrium, where the production rate of stars is about to stop, if right now we have the last Sun-like (G-type) stars been born, then in about 10 billion years from now (this is the life expectancy of a G-type star) all such stars will be gone. If a period of approximately 200 million years was sufficient for dinosaurs to have evolved enough in order to prevent or avoid their extinction (advance enough to become a species with technology and space travel), is a period of 10 billion years long enough for the humankind to invent some technology capable of taking us to another universe (when our universe as we know it will be deprived of all G-type stars)? Or such an option will be the privilege of the most advanced species (as we don’t really know them)?
2.6.3 Our closest neighbors
This is a list of stars within a range of about 15ly:
The nearest stars, their distances in light-years, spectral types and known planets
The nearest stars to Earth are in the Alpha Centauri triple-star system, about 4.37 light-years away. One of these stars, Proxima Centauri, is slightly closer, at 4.24 light-years.
Of all the stars closer than 15 light-years, only two are spectral type G, similar to our sun: Alpha Centauri A and Tau Ceti. The majority are M-type red dwarf stars.
Only nine of the stars in this area are bright enough to be seen by the naked human eye from Earth. These brightest stars include Alpha Centauri A and B, Sirius A, Epsilon Eridani, Procyon, 61 Cygni A and B, Epsilon Indi A and Tau Ceti.
Barnard’s Star, a red dwarf 5.96 light-years away, has the largest proper motion of any known star. This means that Barnard’s Star moves rapidly against the background of more distant stars, at a rate of 10.3 seconds of arc per Earth year.
Sirius A is the brightest star in Earth’s night sky, due to its intrinsic brightness and its proximity to us. Sirius B, a white dwarf star, is smaller than Earth but has a mass 98 percent that of our sun.
In late 2012, astronomers discovered that Tau Ceti may host five planets including one within the star’s habitable zone. Tau Ceti is the nearest single G-type star like our sun (although the Alpha Centauri triple-star system also hosts a G-type star and is much closer).
The masses of Tau Ceti’s planets range from between two and six times the mass of Earth.
[http://www.space.com/18964-the-nearest-stars-to-earth-infographic.html]
This is a wider range of stars within a radius of 50y:
This is a map of every star within 50 light years visible with the naked eye from Earth. There are 133 stars marked on this map. Most of these stars are very similar to the Sun and it is probable that there are many Earth-like planets around these stars. There are roughly 1400 star systems within this volume of space containing 2000 stars, so this map only shows the brightest 10% of all the star systems, but most of the fainter stars are red dwarfs.
[http://www.atlasoftheuniverse.com/50lys.html]
The closest exoplanet to our solar system is Proxima Centauri b:
Artist’s conception of the surface of Proxima Centauri b. The Alpha Centauri binary system can be seen in the background, to the upper right of Proxima.
Proxima Centauri is an exoplanet orbiting within the habitable zone of the closest star to the Sun-the red dwarf star Proxima Centauri, which is in a triple star system. It is located about 4.2 light-years from Earth in the constellation of Centaurus, making it the closest known exoplanet to the Solar System. Proxima Centauri b orbits the star at a distance of roughly 0.05 AU with an orbital period of approximately 11.2 Earth days, and has an estimated mass of at least 1.3 times that of the Earth.
Its habitability has not been established, though it is unlikely to be habitable since the planet is subject to stellar wind pressures of more than 2,000 times those experienced by Earth from the solar wind. The exoplanet is close enough to its host star that it might be tidally locked. In this case, it is expected that any habitable areas would be confined to the border region between the two extreme sides, generally referred to as the terminator line, since it is only here that temperatures might be suitable for liquid water to exist.
The European Southern Observatory estimates that if water and an atmosphere are present, a far more hospitable environment would result. Assuming a world including oceans with average temperatures and atmospheric pressure similar to those on Earth, a wide equatorial belt (non-synchronous rotation), or the majority of the sunlit side (synchronous rotation), would be permanently ice-free. A large portion of the planet may be habitable if it has an atmosphere thick enough to transfer heat to the side facing away from the star. The planet may be within reach of telescopes and techniques that could reveal more about its composition and atmosphere, if it has any.
The discovery of the planet was announced in August 2016 by the European Southern Observatory. The planet was found using the radial velocity method, where periodic Doppler shifts of spectral lines of the host star suggest an orbiting object. According to Guillem Anglada‐Escudé, its proximity to Earth offers an opportunity for robotic exploration of the planet with the Starshot project or, at least, in the coming centuries.
[https://en.wikipedia.org/wiki/Proxima_Centauri_b]
While Proxima Centauri b is not so much promising, as the planet Mars in our own solar system seems to be much more hospitable than Proxima Centauri b, the most promising exoplanets at the moment are the following:
List of exoplanets in the conservative habitable zone:
| Planet | Star | Spectral type | Radius (Earth radii) |
Orbital period (days) |
Distance (ly) |
| Earth | Sun | G2V | 1 | 365 | - |
| Kepler-452b | Kepler-452 | G2V | 1.50 | 385 | 1,402 |
| Kepler-1638b | Kepler-1638 | G4V | 1.60 | 259 | 2,492 |
| Kepler-62f | Kepler-62 | K2V | 1.41 | 267 | 1,200 |
| Kepler-442b | Kepler-442 | K?V | 1.34 | 112 | 1,292 |
| Kepler-186f | Kepler-186 | M1V | 1.17 | 130 | 561 |
In the previous table sorting was done with respect to the spectral type of the star. We see that the closest Earth analog (a bit larger than the Earth), which is also the closest Solar analog (star with exactly the same spectral type with our Sun) is Kepler 452b, at a distance of about 1,400ly. The second closest Earth analog, Kepler-1638b, at a distance of approximately 2,500ly, is more than 1,000ly further away. The next couple of exoplanets (Kepler-62f and Kepler-442b), which are orbiting stars a bit dimmer (spectral type K) than our Sun, are approximately as much distant as the previous two exoplanets (the average distance of these four exoplanets is about 1,600ly). The last of them (Kepler-186f), which incidentally is the closest, although it is an Earth analog, it is not a Solar analog (M-type stars are red dwarfs, much dimmer than the Sun).
Wikipedia also offers a list of exoplanets in the optimistic habitable zone, less likely to have a rocky composition or maintain surface liquid water. Within a range of 50ly there are 12 candidate exoplanets. Of those 12 exoplanets, just two are supposed to be orbiting a star similar to our Sun (spectral type G), Tau Ceti e, at a distance of 12ly, and HD 20794 e, orbiting the star 82 G. Eridani, 20ly away (both these planets are given as unconfirmed).
This is a table with some possible frequencies:
| Total number of stars (within 50ly) |
2,000 | |
| Number of stars which are Sun-like | fs≈ 0.1 | 1,200 |
| Number of those stars with Earth-like planets | fp≈ 0.1 | 20 |
| Number of those planets which are found in the habitable zone | fh≈ 0.1 | 2 |
| Number of those habitable planets which may be life-bearing | fl≈ 0.1 | 0.2 |
In the previous table each next frequency is declining by an order of 10. The 2 exoplanets corresponding to the frequency fh could be those already mentioned (the planets in Tau Ceti and 82 G. Eridani).
However such a result seems to be quite optimistic. If the closest Earth and Solar analog (an Earth-like planet orbiting a Sun-like star in the habitable zone), which potentially supports life (Kepler 452b), is 1,400ly away from us, then supposing that there are 56,000 stars within that range (about 30 times the number of stars at a distance of 50ly), the probability of such an exoplanet (both an Earth and Solar analog) will be 1.8×10-5 (1/56,000). If we include all the 4 Earth-like habitable planets (orbiting both G-type and K-type stars), then for an average distance of 1,600ly, thus for a number of 64,000 stars, the same probability will be 6.25×10-5 (4/64,000 or 1/16,000). Thus one such exoplanet on average for 16 thousand stars. The number of Earth-like habitable planets could be 5 times higher if we include red dwarfs (since red dwarfs are 5 times more populous than Sun-like stars), but probably the frequency of life as we know it will not increase (since it is doubtful whether red dwarfs can sustain life). While the closest ‘interesting’ exoplanet is Tau Ceti e, just 12ly away (or even Proxima Centauri b at 4.2ly), the most promising exoplanets are at least 1,400ly away.
Even if we assume that in the future we will discover many more exoplanets, the data of exoplanets already known suggests by analogy (if the sample we already have is representative) that the ratios will not change significantly. Thus, given the data, the frequency fh≈10-4-10-5, referring to the number of Earth-like planets orbiting Sun-like stars in the habitable zone, gives us an idea about the orders of magnitude involved- not to mention that the frequency fl, the number of Earth-like habitable exoplanets on which life has indeed appeared, will probably be at least an order of magnitude lower than fh.
Here we may gather some of the facts with respect to Drake frequencies:
3.1 Exponential vs logistic growth
The rate R* of new stars is approximately equal to 1 if we also include the rate of stars which disappear. Thus we may assume that right now the Milky Way is at a state of equilibrium, with almost the maximum number of stars. Thus R* can be set equal to 1, or assuming that the number L* represents the lifespan of a star (instead of the lifespan of a civilization), then the product N*= R*L* will give us the total number of stars (N*=100 billion stars).
Not all of these MS (main sequence) stars may be suitable for life as we know it. The habitability of red dwarf star systems is disputed for many reasons. The most important reason may be the energy deficiency of such stars, whose luminosity is no more than 10% that of the Sun. The aspect that they last much longer than the Sun (up to trillions of years) has no meaning if G-type stars like our Sun will be all gone after, let’s say, 10 billion years from now. This is why the frequency fs was introduced, representing the percentage of MS stars which are Sun-like. By ‘Sun-like’ it is meant stars with mass close to that of the Sun (let’s say 0.7-1.3 solar masses). This includes, together with G-type stars like our Sun, the lightest F-type stars, and the heaviest K-type stars. The frequency fs is about 10%, or no more than 20%.
The frequency fp, giving the percentage of stars (Sun-like or not) with planets depends on the data currently available. To make an estimation we can use Wikipedia’s full list of exoplanets, assuming a range of 50ly:
[https://en.wikipedia.org/wiki/List_of_exoplanets_(full)]
According to this list (for many planets the distances are not given), within a range of 50 light years there are 111 exoplanets. Within this range there are 2,000 stars, 200 of which are Sun-like. Thus approximately 5.55% (111/2000) of all the 2,000 stars within a range of 50ly has planets. This gives us fp= 0.055≈ 0.1.
Additionally, of those 111 exoplanets, 6 are given as potentially habitable. Thus 5.4% (6/111) of all the 111 planets within a range of 50ly may be habitable. Thus the percentage of potentially habitable (presumably also terrestrial) exoplanets is fh= 0.054≈ 0.1.
Incidentally none of the previous 111 habitable exoplanets is orbiting a Sun- like star. As we previously saw, the closest Earth and Solar analog right now (Kepler 452b) is located almost 1,500ly away, among at least 6,000 stars (at least 3 times as many as the 2,000 stars within 50ly). Thus the percentage fh of habitable Earth-like exoplanets orbiting Sun-like stars drops from fh ≈ 10-1 (about 6 habitable Earth-like exoplanets in 2,000 stars within a range of 50ly) to no more than fh= 1/6,000= 0.000167≈ 10-4 (1 habitable Earth-like exoplanet orbiting a Sun-like star in 6,000 stars).
Therefore although it has been estimated (as mentioned earlier) that as many as 40 billion Earth-like exoplanets may be orbiting in the habitable zones of Sun-like stars and red dwarfs within the Milky Way (fh =40% for a total of 100 billion stars), and that 11 billion of these planets may be orbiting Sun-like stars (fh ≈10% if we only account for Sun-like stars), such estimations seem to be at least an order of magnitude too optimistic.
As far as the frequencies fl and fi are concerned, no data exist. We may suppose that life in the universe is abundant, in the sense that microbial life may begin from very basic chemical elements, if the conditions are right. However if the conditions are not met (e.g. right temperature and atmospheric pressure, presence of liquid water, etc.), life may never be given the opportunity to appear. Even if we consider that all conditions are right on a potentially habitable exoplanet, exoplanetary factors (e.g. solar radiation, volcanism, supernova explosions, comet impacts, etc.) could have made it impossible for life to thrive. On the other hand, if life on an exoplanet has indeed appeared and thrived, it is doubtful that it has evolved into intelligent species. And by this it is meant a civilization, not just dinosaurs.
Here is an example of how the frequency fl might be estimated by analogy:
Here is a similar example with respect to the frequency fi:
Ratio (Evolutionary stage/Earth’s age)
|
fi
|
Homo Erectus (2,000,000ya)
|
4.44×10-4
|
Homo Sapiens (200,000ya)
|
4.44×10-5
|
First civilizations- Neolithic Revolution (10,000ya)
|
2.22×10-6
|
Industrial Revolution (200ya)
|
4.44×10-8
|
Modern Technological Era: (30ya, beginnings of SETI)
|
6.66×10-9
|
If there could be as many as 40 billion Earth-like planets (as earlier mentioned) in the habitable zone of their stars, about 4 billion of them could host life in the form of complex multicellular organisms, 18 million could be inhabited by ape-like creatures like Homo Erectus, there could be as many as 1,800 civilizations at the stage of industrialization, or about 250 civilizations with their own SETI programs.
This is a summary of the existing data previously mentioned (with respect to the frequencies fs, fp, and fh):
Distance from the Earth: 50ly.
Number of stars within that distance: 2,000.
Number of those stars which are Sun-like: 200.
Frequency of Sun-like stars: fs= (200/2,000)= 0.1= 10-1.
Number of Earth-like planets (including all the stars): 111.
Frequency of Earth-like planets: fp= (111/2,000)= 0.0555= 5.55×10-2≈ 10-1.
Number of potentially habitable Earth-like planets: 6.
Frequency of potentially habitable Earth-like planets (orbiting all MS stars):
fh= (6/111)= 0.054= 5.54×10-2 ≈10-1.
Frequency of potentially habitable Earth-like planets (orbiting only Sun-like stars):
fh= (1/6,000)= 0.0167= 1.67×10-2≈ 10-2.
Number of habitable Earth-like planets with life: ?
Number of habitable Earth-like planets with intelligent life: ?
A characteristic of the previous data is the repetitive nature of the successive frequencies, where for the frequencies fs, fp, and fh the order of magnitude 10-1 (with respect to the previous frequency) is the same. Supposing that the same is true for the rest of the frequencies fl and fi, here is a related table:
Total number of stars in the Milky Way
|
100 billion MS stars
|
|
Frequency of stars which are Sun-like
|
fs= 0.1= 10-1
|
10 billion Sun-like stars
|
Frequency of Sun-like stars with Earth-like planets
|
fp= 0.055= 5.5×10-2≈
10-1
|
1 billion planets
|
Frequency of those planets in the habitable zone
|
fh= 0.054= 5.4×10-2
≈10-1
|
100 million habitable planets
|
Frequency of those planets
with life
|
fl≈ 10-1?
|
10 million life-bearing planets?
|
Number of those planets with intelligent life
|
fi≈ 10-1?
|
1 million planets with intelligent life?
|
The previous table may be considered over-optimistic. For example if there are 1 million planets with intelligent life, then there could be as many as 100 thousand civilizations out there (fc= 0.1) able to communicate. However so many advanced civilizations seem to be absent.
Another way to treat the Drake frequencies is to assume that each next frequency is the product of the previous couple of frequencies (considering thus a Fibonacci product of the frequencies). This is a related table:
Drake’s frequencies
|
Fibonacci product
(optimistic)
|
Total number of MS stars in the Milky Way (100 billion)
|
Law of squares
(conservative)
|
Total number of MS stars in the Milky Way (100 billion)
|
fS: Number of stars which are Sun-like
|
fS= 2×10-1
|
20 billion
Sun-like stars
|
fS= 2×10-1
|
20 billion
Sun-like stars
|
fP: Number of Sun-like stars with Earth-like planets
|
fP= fS×fS=
4×10-2
|
4 billion
Earth-like planets
|
fE= ( fS)2=
4×10-2
|
4 billion
Earth-like planets
|
fH: Number of Earth-like planets in the habitable zone
|
fH= fS×fP=
8×10-3
|
800 million
habitable planets
|
fH= (fE)2=
16×10-4
|
160 million
habitable planets
|
fL: Number of those planets with life
|
fL= fP×fH=
32×10-5
|
32 million
planets with life
|
fL= (fH)2=
256×10-8
|
256 thousand
planets with life
|
fI: Number of those planets with
intelligent life
|
fI= fH×fL=
256×10-8
|
256 thousand
civilizations
|
fI= (fH)2=
65,536×10-16
|
1 civilization
(as we know it)
|
fC: Number of those intelligent species which are advanced
(can communicate)
|
fC= fL×fI=
8,192×10-13
|
82 advanced civilizations
|
In this table each next frequency (second column) gives the total number corresponding to the frequency (not the percentage with respect to the previous frequency). The second frequency is produced by the first one multiplied by itself.
The factor of 2 before the order of magnitude 10-1 was added in order to give somewhat higher frequencies.
The next to last column (law of squares) treats each next frequency as the square of the previous one (thus these frequencies are smaller than those in the second column).
Such sequences of frequencies are produced on a theoretical basis, and variations can be used in order to fit into any contemporary observations, as the purpose of those sequences is mostly illustrative, rather than to be taken literally.
But interestingly enough, using the law of squares, the frequency fi (4th column, 6th raw) gives a result approximately equal to 1 (there is 1 intelligent species in the Milky Way, and this species is us).
The low values of the frequencies can be interpreted in two alternative ways. On one hand, our current technology may be inadequate to trace life-bearing planets and communicate with other civilizations. On the other hand, this could be the dawn of civilizations in the history universe, so that it is too early to trace them and communicate with them. In fact even if a few advanced civilizations appear then the frequencies fl and fi will go upwards, considering that the rate with which those civilizations will terraform other planets and help other species to advance, will be much greater than the physical rate.
But perhaps the true problem is not the estimation of the frequencies in space and time, but the way we perceive space and time. This is an example: There are about 100 billion stars in the Milky Way, and about 100 billion galaxies in the universe. If there is just 1 civilization per galaxy in the universe, then there will be as many civilizations as the number of galaxies in the universe, or as many as the stars in the Milky Way (1011= 100 billion). Additionally if we suppose that there are as many universes in the multiverse as the number of galaxies in our universe, or as many as the stars in our own galaxy, then there will be 1011×1011=1022 civilizations in the multiverse. Furthermore, we may suppose that the multiverse is just a cluster of universes of an even larger distribution, and so on, so that the number of civilizations in an endless distribution of spacetime will practically approach infinity. Now we might argue that although the number of civilizations may be very large, the distance between them will also be very large. But if we suppose that, despite the infinite distances, there are wormholes which connect distant places in space instantaneously, then a civilization using the wormholes could visit other civilizations right away. Therefore there would be an infinite number of civilizations out there, and an infinite number of choices, considering whom to visit.
Here we will assume non- linear approaches (exponential, logistic, and Gaussian) to Drake’s equation. We will also introduce the normal distribution, see that MS stars are with a good approximation normally distributed according to their type (thus also their mass), so that we will suppose that civilizations living in those star systems will also be normally distributed according to their own type (given by Kardashev’s scale). We will also use the solar mass analog in order to find a relationship between the spectral type of the star and the Kardashev type of a civilization in that star system.
Two modes of population growth. The exponential curve (also known as a J-curve) occurs when there is no limit to population size. The logistic curve (also known as an S-curve) shows the effect of a limiting factor (in this case the carrying capacity of the environment).
[https://www2.estrellamountain.edu/faculty/farabee/biobk/BioBookpopecol.html]
If we accept the observation that our Milky Way galaxy is reaching a state of equilibrium (the rate of new stars is approaching zero, thus the number of stars is approaching the maximum value), and we also assume that the time difference between the birth of a star and the appearance of intelligent life in the same star system is about 5 billion years (as long as it took us to appear), then we may expect a rapid increase in the number of emerging intelligent species in the next 5 billion years. This period of time may be much less if we assume an exponential growth of civilizations in the Milky Way.
Returning to Drake’s equation,
where Pj is the product of Drake’s frequencies fj, if we set
we take that
where R is the production rate of civilizations, equal to the production rate R* of new stars multiplied by the product Pj of Drake’s frequencies fj.
This simply tells us that the number of civilizations N is proportional to their lifespan L, where the constant of proportionality is the growth factor k.
Incidentally the constant k may also be identified with the product Pj of Drake’s frequencies, if the production rate of stars R* is about equal to 1,
The point here is that the equation
is the linear approximation of the function
for small values of the growth factor k. In fact L has units of time t. The previous function describes exponential growth, and it is derived from the following differential equation
where it is assumed that the number N of a species increases proportionally to the number of species present at a given point in time t.
This differential equation is solved as follows,
If we suppose that at some starting time t= 0, the initial population is N0= 1, the previous equation takes the simpler form
If now we set
then the linear approximation of the previous function for x≈ 0 is
Therefore the function N= kt≡ kL, L≡t, is the linear approximation of the function N=ekt, either if k is sufficiently small (for any time t), or if t is sufficiently small (for any value of k). But even if the growth factor is small, as time evolves, sooner or later the exponential function will start to significantly deviate from its linear approximation, as exponential functions generally increase rapidly.
In order to estimate the population at some future time t, the growth factor k has to be determined. If we solve the exponential function for k, we have
The problem here is that in order to determine the value of k we have to know the number of species N at some point in time t. This cannot be done at the moment, since the only species (civilization) in the Milky Way which we are aware of is our own. However an estimation of k can be done if we assume that the growth factor k is proportional to the product Pj of Drake’s frequencies fj:
If we use for the value of k Drake’s ‘educated guesses,’ which we have already seen,
R* = 1,
fp = 0.2- 0.5,
ne = 1- 5,
fp×ne≈ 1,
fl = 1,
fi = 1,
fc = 0.1- 0.2≈ 0.15,
we take that
we take that
If we use this value for k,
and suppose that right now, t= 0, there is just 1 civilization (us) in the Milky Way galaxy, N0= 1, then there will be as many civilizations as the stars in the Milky Way (100 billion) in just 100 years:
The improbability of such a result tells us that the growth factor k has to be much smaller. Thus if we alternatively use the frequencies of the Fibonacci product, which we earlier saw,
fS= 2×10-1≈
10-1
|
fP= fS×fS=
4×10-2≈ 10-2
|
fH= fS×fP=
8×10-3≈ 10-2
|
fL= fP×fH=
32×10-5≈ 10-4
|
fI= fH×fL=
256×10-8≈ 10-6
|
fC= fL×fI=
8,192×10-13≈ 10-9
|
then we take for the growth factor (frequency of civilizations able to communicate),
Supposing again that all 1011 star systems could be inhabited at some future time t, then this time will be
The significance here is not the exact time when the peak population might occur, but the order of magnitude of that time. Although such a time could really be in the order of billions of years, the growth factor can be increased in the future if the first advancing civilizations begin to terraform other planetary systems, or even create life on them. If for example we suppose that there is just 1 highly advanced civilization in the Milky Way at present, and that it will take that civilization 50,000ly to colonize all the star systems in the Milky Way (since the Milky Way has a radius of about 50,000ly, an advanced civilization spreading at the speed of light radially from its place of origin will reach the edges of the Milky Way in 50,000 years), then the growth factor will be,
With that growth rate, such an advanced civilization will have colonized all the 100 billion stars of the Milky Way in 50,000- 100,000 years.
Three models of population growth: Linear (green line), exponential (red line), and logistic (orange line).
Although civilizations in the Milky Way as soon as they appear may grow and expand rapidly, there are limitations to be accounted for. Such a limitation is the environment’s capacity, as the stars in the Milky Way, as well as the energy resources, are finite. Thus exponential growth may not occur forever. A more plausible model of growth is that of logistic growth. The formula of logistic growth is
where N is the population at some time t, N0 is the maximum population, and k is the growth factor. The main aspect of logistic growth is that, as the previous graph illustrates, the growth of a population increases exponentially in the beginning, but reaches a turning point after which growth is decelerated, until the population reaches the maximum capacity, at which point population growth becomes zero.
The three functions of linear (green line), exponential (red line), and logistic (orange line) growth presented in the previous graph are respectively,
For the growth factor k it was assumed a value such that after a time about equal to t=100,000 years, the population will reach its peak N0= 100 billion civilizations, corresponding to the 100 billion stars in the Milky Way galaxy (either all stars will be occupied by civilizations independently, or, alternatively, that the first advanced civilizations will colonize all the stars in the Milky Way). The maximum number N0 can also be seen as a percentage (100%). The time t0 corresponds to N(t)= N0/2 in the logistic function. Thus at that time, which is equal to t0= 50,000 years, half of all the species will be present. Explicitly, for the given values of k=10-4, N0= 100, and t0= 50,000, the logistic function is
We see in the graph that the logistic function after the midpoint, at t= t0, turns around and decelerates towards the peak population N0. Probably at an initial stage civilizations will start to emerge in the Milky Way at an exponential rate. Further on, various constraints, including energy resources or extinction events, will eventually slow down the pace of new civilizations.
Another aspect is that the first sufficiently advanced civilizations will colonize other star systems, presumably assimilating already existing but less advanced civilizations in those star systems. If a superior civilization appears in the Milky Way then it is possible that this civilization will absorb all others, creating thus a single globalized civilization all across the Milky Way, whatever the local differences might be. However the same constraints (wars and energy resources) might break apart such an intergalactic empire, so that we had better assume an average density of independent civilizations in the Milky Way. The radius of influence of a civilization (sufficiently advanced to have occupied its neighboring solar systems) which will define the population density, thus also the maximum number of civilizations, is a matter of guess. For example, approximating the Milky Way with a cylinder, with a radius (length) R=50,000ly, and an average height h=1,000ly, then for the thin disk area A and the volume V of the Milky Way we have, respectively,
If on the other hand we assume that the average radius r at which a civilization will expand is, let’s say, 30ly, each civilization will occupy on average a volume Vr (a sphere of radius r),
so that the maximum possible number of civilizations will be
thus about 70 million different civilizations.
A significant point to mention here is that because the order of magnitude of the distances in the Milky Way (≈105ly) is much greater than the order of magnitude of a species lifetime (in the case of the human lifetime ≈102), ‘speciation’ may be favored versus ‘colonization.’ For example, if the speed of light is an upper limit for interstellar travel, from our place in the Milky Way, which is about 25,000 light years from the center of the galaxy, and since the radius of the Milky Way is about 50,000ly, it would take us 75,000 years to travel to the far end of our galaxy, supposing that we had the technology to travel at the speed of light. But after a total of 150,000 years to make the journey forth and back, the returning space travelers may hardly recognize the species they once left behind (the rest of us). If they never come back, and settle somewhere at the edge of the Milky Way, the spacetime separation of 75,000 years may be sufficient for them to become a different species. Even if we suppose a constant communication between them and the Earth during their travel, the ‘here and now’ will become more and more distant between them and the Earth, so that finally communication will break down. Therefore, on one hand the number of civilizations may increase by expansion and speciation, while on the other hand the number of civilizations may decrease by colonization and assimilation (or extermination).
Even so, even in the most idyllic case, where a large number of civilizations may live peacefully in their own planetary systems within their sphere of influence, stars will not last forever. If the Milky Way is now at equilibrium (minimum production rate of stars, maximum number of stars), Sun-like (G-type) stars will die out after about 10 billion years. If we assume a maximum population density in the Milky Way after 5 billion years, this density will then begin to decrease, as the number of Sun-like stars will gradually decrease, until all the Sun-like stars will vanish after another 5 billion years, 10 billion years from now. Therefore the number of civilizations, after reaching a plateau (a maximum), will also begin to decrease. Such an aspect cannot be described by logistic growth, but it can be described by a Gaussian function.



















































































































































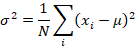








































































































































No comments:
Post a Comment